∑k^4（シグマkの4乗）が出たらどうする？
どの高校数学の教科書でもどの参考書でもどの授業でも \(\displaystyle\sum_{k=1}^n k^3\) までは公式として暗記させるはずです。
めぐろ塾の安田でも君は大学受験で \(\displaystyle\sum_{k=1}^n k^4\) が出題されても大丈夫？
結論：\(\displaystyle\sum_{k=1}^n k^3\) までの公式の証明法をおさえていれば問題ない
君たちが日常的に使っているであろう、 \(\displaystyle\sum_{k=1}^n k^3\) までの公式の証明法をおさえていれば、\(\displaystyle\sum_{k=1}^n k^4\) が出題されても大丈夫です。
因みにこの証明はどの教科書にも載っていますが…
めぐろ塾の安田あんまり証明の核が明文化されてないので、この記事ではそこを解消するね！この記事を理解する上で…
前提となる知識
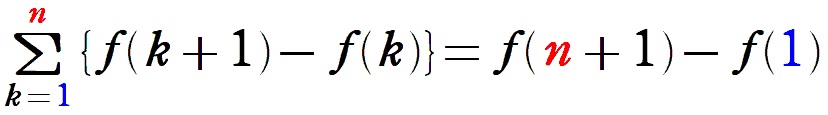
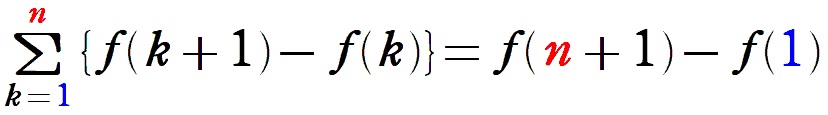
めぐろ塾の安田数列の和ってほとんどこれ↑で計算するのに正式名称はありません(笑)
\(k=1\:～\:n\) でなくても使えるので、\(f(k+1)\) の \(k\) に区間の上を代入、\(f(k)\) の \(k\) に区間の下を代入って公式化しておきましょう！
因みにシグマの中に \(f(k+1)-f(k)\) を作れれば、具体的に和を書き並べると途中が消えるってだけ↓なんですが…
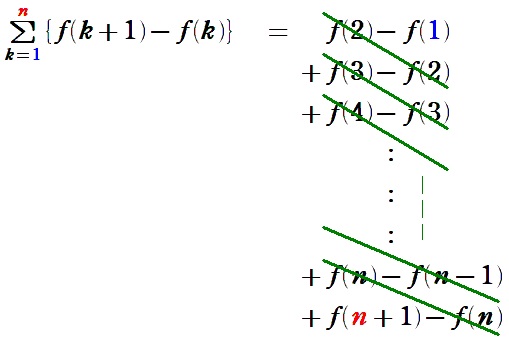
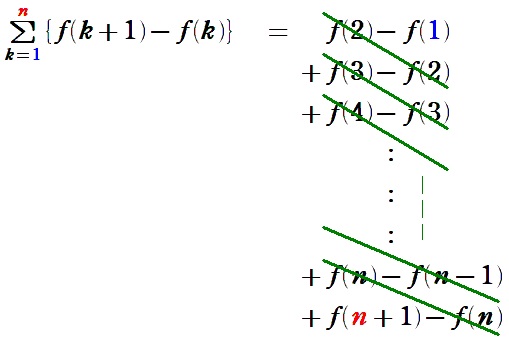
大学受験では一問で複数回使うこともあるんで、公式化せずにいちいち消してる人は凄い不利になります。
\(f(k+1)-f(k)\) とか意味不明～
めぐろ塾の安田って人はめぐろ塾に来なさい↓(笑)懇切丁寧に説明してあげる
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
出題例
めぐろ塾の安田大学受験で出題されてないなら \(\displaystyle\sum_{k=1}^n k^4\) なんて知りたくもないよね(笑)
ってわけでいくつか出題例を。特に医学部で良く目にします。
2014東京医科大
2017獨協医科大
\(\displaystyle\sum_{k=1}^n k^3\) までを証明してみよう！
めぐろ塾の安田繰り返すけど、\(\displaystyle\sum_{k=1}^n k^3\) までの公式の証明法をおさえていれば、\(\displaystyle\sum_{k=1}^n k^4\) が出題されても大丈夫！
君たちが暗記しているであろう↓
累乗の和の公式
(Ⅰ) \(\displaystyle\sum_{k=1}^n c=nc\)（\(c\) は定数）
(Ⅱ) \(\displaystyle\sum_{k=1}^n k=\displaystyle\frac{1}{2}n(n+1)\)
(Ⅲ) \(\displaystyle\sum_{k=1}^n k^2=\displaystyle\frac{1}{6}n(n+1)(2n+1)\)
(Ⅳ) \(\displaystyle\sum_{k=1}^n k^3=\displaystyle\frac{1}{4}n^2(n+1)^2\)
を証明していきましょう！
めぐろ塾の安田因みにこれらを完全暗記してなかったら、数学使って受験しちゃダメだよ(笑)金のムダ！
(Ⅰ) \(\displaystyle\sum_{k=1}^n c=nc\) の証明
当たり前です。具体的に和を書き並べてみるだけ↓
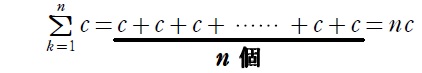
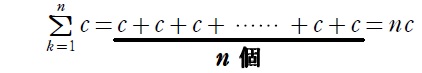
(Ⅱ) \(\displaystyle\sum_{k=1}^n k=\displaystyle\frac{1}{2}n(n+1)\) の証明
めぐろ塾の安田これは等差数列の和としても証明できるんだけど…(Ⅲ)以降に備えて、あえて…
証明したい \(k^●\) の次数を１つ上げて \(f(k)\) とし、
\(f(k+1)-f(k)\) を作る！
ことで証明します。
\((k+1)^2-k^2\:\)\(=2k+1\)
\(k=\displaystyle\frac{(k+1)^2-k^2}{2}-\displaystyle\frac{1}{2}\)
シグマは中の和・差が分解できることを意識すると…
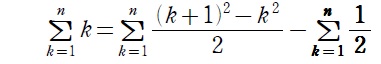
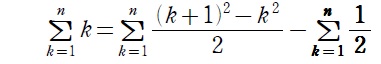
めぐろ塾の安田第１項は先に紹介した「前提となる知識」で、
第２項は公式(Ⅰ)で計算できます。
(Ⅲ) \(\displaystyle\sum_{k=1}^n k^2=\displaystyle\frac{1}{6}n(n+1)(2n+1)\) の証明
めぐろ塾の安田こっからは証明したい \(k^●\) の次数を１つ上げて \(f(k)\) とし、
\(f(k+1)-f(k)\) を作るのが必須。\(k^2\) の次数を１つ上げた \(k^3\) を \(f(k)\) として \(f(k+1)-f(k)\) を計算すると…
\((k+1)^3-k^3\:\)\(=3k^2+3k+1\)
めぐろ塾の安田\(\displaystyle\sum_{k=1}^{n}k^2\) を証明したいから、\(k^2\) について整理
\(k^2=\displaystyle\frac{(k+1)^3-k^3}{3}-k-\displaystyle\frac{1}{3}\)
めぐろ塾の安田両辺にシグマをつければ、
第１項は「前提となる知識」で、
第２項はさっき証明した公式(Ⅱ)で、
第３項は公式(Ⅰ)で計算できます。
(Ⅳ) \(\displaystyle\sum_{k=1}^n k^3=\displaystyle\frac{1}{4}n^2(n+1)^2\) の証明
めぐろ塾の安田もう機械作業にできるでしょ(笑)
\(k^3\) の次数を１つ上げた \(k^4\) を \(f(k)\) として \(f(k+1)-f(k)\) を計算して \(k^3\) について整理
\((k+1)^4-k^4\:\)\(=4k^3+6k^2+4k+1\)
めぐろ塾の安田因みにここからは展開に「二項定理」or「パスカルの三角形」を使っちゃいます。「二項定理」についてはこの記事のここで説明してるから、上の展開できない人は読んでみて！
\(k^3=\displaystyle\frac{(k+1)^4-k^4}{4}-\displaystyle\frac{3}{2}k^2-k-\displaystyle\frac{1}{4}\)
めぐろ塾の安田両辺にシグマをつければ、
第１項は「前提となる知識」で、
第２項はさっき証明した公式(Ⅲ)で、
第３項はさっき証明した公式(Ⅱ)で、
第４項は公式(Ⅰ)で計算できます。
\(\displaystyle\sum_{k=1}^n k^3\) までの証明のまとめ
結局これらの証明で大事なのは、
証明したい \(k^●\) の次数を１つ上げて \(f(k)\) とし、
\(f(k+1)-f(k)\) を作る！
↓
前の公式から、段階的に証明していける！
めぐろ塾の安田ってこと。これさえ分かってれば…
\(\displaystyle\sum_{k=1}^n k^4\) が出ても大丈夫
\((k+1)^5-k^5\:\)\(=5k^4+10k^3+10k^2+5k+1\)
めぐろ塾の安田\(k^4\) について整理すれば…
\(k^4=\displaystyle\frac{(k+1)^5-k^5}{5}-2k^3-2k^2-k-\displaystyle\frac{1}{5}\)
めぐろ塾の安田両辺にシグマをつければ、
第１項は「前提となる知識」で、
第２項は知ってる公式(Ⅳ)で、
第３項も知ってる公式(Ⅲ)で、
第４項も知ってる公式(Ⅱ)で、
第５項は当たり前の公式(Ⅰ)で計算できるってこと
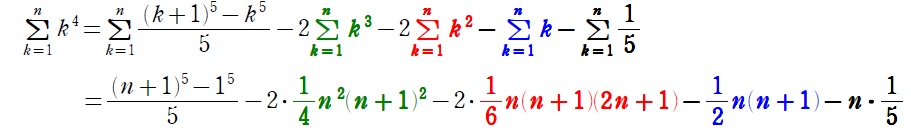
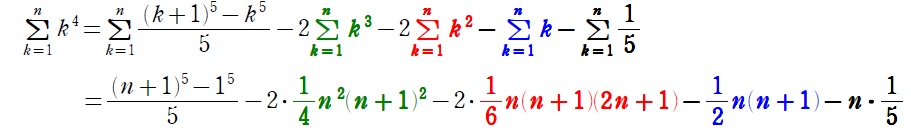
めぐろ塾の安田因みに出題例からも分かる通り、これを因数分解した形で解答することはほとんどないから、ここまでできれば大丈夫です。でも一応興味ある人のために因数分解もしておく↓(笑)
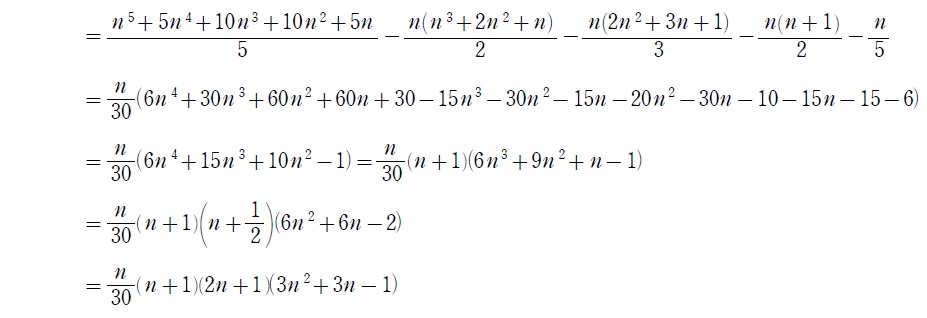
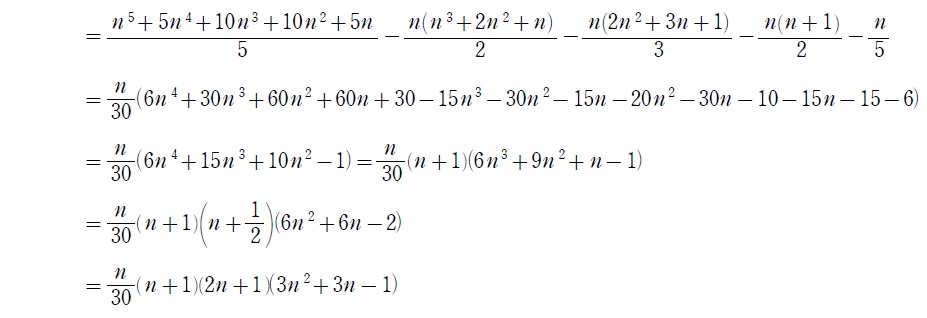
まとめ
めぐろ塾の安田長ったらしく説明してきましたが…
\(\displaystyle\sum_{k=1}^n k^3\) までの公式の証明法をおさえていれば、\(\displaystyle\sum_{k=1}^n k^4\) が出題されても大丈夫です。
めぐろ塾の安田でも出題例で挙げてる問題は共に10分使えないから、医学部受験者は何度かやって慣れといた方がいいと思う。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
君の大学受験が最高の結果になることを祈ってます！
