「三角関数の公式」はどれを覚えるべき?

三角関数って公式が多いから苦手…
って人は多いでしょう。
 めぐろ塾の安田
めぐろ塾の安田安心して。数学のプロ講師の僕も高2の頃までチョー苦手だった(笑)
僕が苦手だった理由を今解析すると…
どれは丸暗記し、どれは導出すべきなのか
が明文化されてないから!
教える人によっても「覚えろ」・「導出しろ」の基準が全然違うんですよね…



僕は高2の頃、学校=暁星高校の先生に「積和・和積公式も覚えろ!」って言われて、「こんな複雑なの8つも覚えられないよ…」って感じで苦手になっちゃいましたね(笑)
2023共通テスト第1問がそうしているように、積和・和積公式は暗記せずに導くのが常識とされています。
とゆ~わけでこの記事では…



「ごく平均的な頭の持ち主」=「私め」が、20年の講師歴に基づき…
大学受験に向けて一般の生徒が、三角関数の公式のどれを丸暗記し、どれは導出すべきなのかを、理由付きで明文化して差し上げますm(_ _)m
三角関数の定義と相互関係
三角関数の定義(絶対に暗記!)
1999東大で「これを述べる」→「加法定理の証明」が出題されて話題になりました。
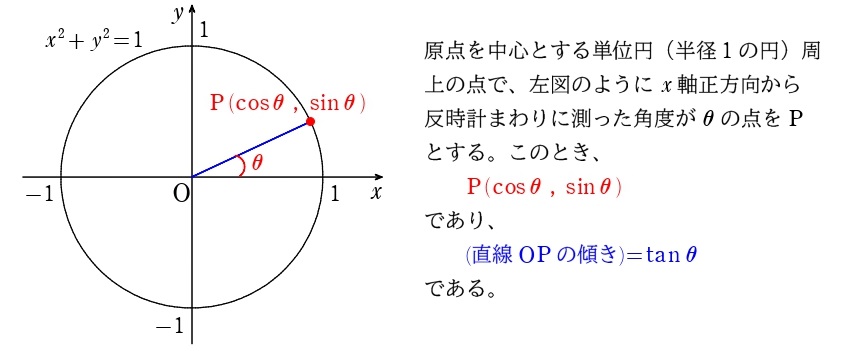




カンタンに言うと、単位円周上の…
- \(x\) 座標が \(\cos\theta\) で \(y\) 座標が \(\sin\theta\)
- 傾きが \(\tan\theta\)
ってだけです。これさえしっかり暗記しておけば…
相互関係(覚えないけど覚えちゃう)
三角関数の相互関係
\[\begin{split}&①\;\;\sin^2\theta+\cos^2\theta=1\\&②\;\;\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\\&③\;\;1+\tan^2\theta=\displaystyle\frac{1}{\cos^2\theta}\end{split}\]



の①と②は当たり前なので覚えません!…まぁ…使いすぎて覚えちゃうんですが(笑)
\(\textrm{P}\;(\cos\theta\;,\;\sin\theta)\) は単位円 \(x^2+y^2=1\) 上の点だから、代入して \(\cos^2\theta+\sin^2\theta=1\) が成立、つまり①の成立は当たり前。
(傾き)=(\(y\) の変化量)/(\(x\) の変化量) だから、\(x\) 座標が \(\cos\theta\) で \(y\) 座標が \(\sin\theta\) を意識すれば、\(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\) 、つまり②は当たり前。
③は、①と②を用いることで、
\[\begin{split}1+\tan^2\theta&=1+\displaystyle\frac{\sin^2\theta}{\cos^2\theta}=\displaystyle\frac{\cos^2\theta+\sin^2\theta}{\cos^2\theta}\\&=\displaystyle\frac{1}{\cos^2\theta}\end{split}\]
と導けますが…
| \(③\;\:1+\tan^2\theta=\displaystyle\frac{1}{\cos^2\theta}\) は… | |
|---|---|
| 理系生徒 | \(\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x^2}dx=\displaystyle\frac{\pi}{4}\) といったアークタンジェント系の積分、\(I_n=\displaystyle\int_{0}^{\frac{\pi}{4}}\tan^nxdx\) で \(I_n+I_{n+2}=\displaystyle\frac{1}{n+1}\) という漸化式を導くときに使うので、絶対に丸暗記! |
| 文系生徒 | 上位校で \(\sin\theta\;,\;\cos\theta\) を \(\tan\displaystyle\frac{\theta}{2}=t\) で表すときに使うくらいだから、暗記しなくて良し! |
となります。
負角・補角とその関連公式 絶対に暗記しちゃダメ!



これらは絶対に暗記しちゃダメ!
定義(単位円)から導きましょう!
負角・補角公式
負角公式
\[\begin{split}&\sin(-\theta)=-\sin\theta\\&\cos(-\theta)=\cos\theta\\&\tan(-\theta)=-\tan\theta\end{split}\]
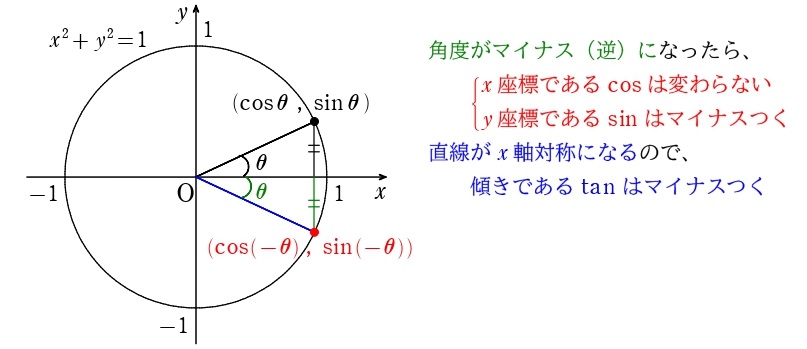




ってだけです。補角公式も同様↓
補角公式
\[\begin{split}&\sin(\pi-\theta)=\sin\theta\\&\cos(\pi-\theta)=-\cos\theta\\&\tan(\pi-\theta)=-\tan\theta\end{split}\]
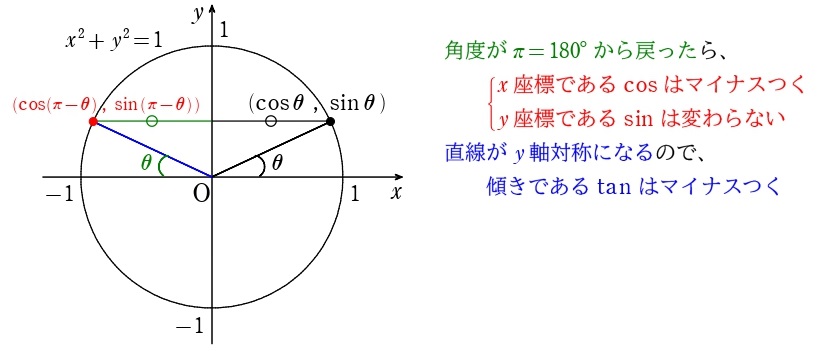

関連公式
負角・補角公式と関連して、公式として紹介している教科書も多いものを紹介します。



やはり絶対に暗記しちゃダメ!
まずこれ↓は負角・補角と同様。
\[\begin{split}&\sin(\theta+\pi)=-\sin\theta\\&\cos(\theta+\pi)=-\cos\theta\\&\tan(\theta+\pi)=\tan\theta\end{split}\]





これ↓は合同な直角三角形の作成を意識して導くといいです。ってか導けなくても加法定理で計算できるから問題なし(笑)
\[\begin{split}&\sin\left(\theta+\displaystyle\frac{\pi}{2}\right)=\cos\theta\\&\cos\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\sin\theta\\&\tan\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\displaystyle\frac{1}{\tan\theta}\end{split}\]


余角公式 言葉で丸暗記!
直前の内容と同様にして、余角公式↓が導けます。



tanは大学受験ではほぼほぼ使わないので割愛しますm(_ _)m
余角公式
\[\begin{split}&\sin\left(\displaystyle\frac{\pi}{2}-\theta\right)=\cos\theta\\&\cos\left(\displaystyle\frac{\pi}{2}-\theta\right)=\sin\theta\end{split}\]
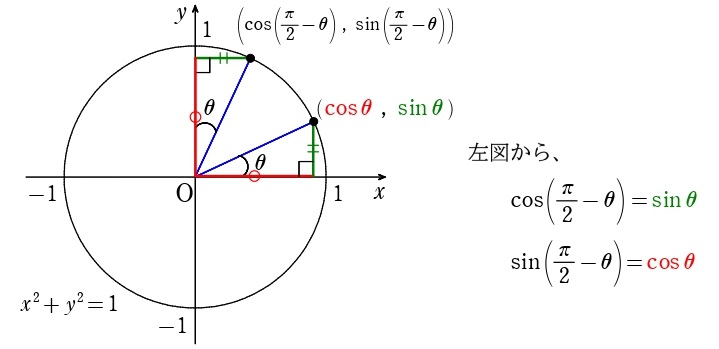




これらは逆に使うと…
\(\displaystyle\frac{\pi}{2}=90^{\circ}\) から元の角度を引けば、
sinとcosは変え放題!
ということになり、和積公式を使うための下準備等で用いることになるので、式ではなく↑の言葉を丸暗記してください!
加法定理 絶対に丸暗記!



っつ~か丸暗記できないなら数学使って受験しちゃダメ(笑)使いどころは多すぎて列挙する気も起きない…
証明は1999東大が出しちゃってるので、もう出ないと思うから割愛しますm(_ _)m
加法定理
\(\sin(\alpha+\beta)=\)\(\;\sin\)\(\alpha\)\(\;\cos\)\(\beta\;+\)\(\;\cos\)\(\alpha\)\(\;\sin\)\(\beta\)
咲いたコスモス、コスモス咲いた
\(\cos(\alpha+\beta)=\)\(\;\cos\)\(\alpha\)\(\;\cos\)\(\beta\;-\)\(\;\sin\)\(\alpha\)\(\;\sin\)\(\beta\)
コスモスコスモス、咲いた咲いた
\(\tan(\alpha+\beta)=\displaystyle\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)
いちひくたんたんたんぷらたん
↑の語呂合わせで、
- \(\alpha\) と \(\beta\) は順番通り書く!
- 角度がマイナスの場合、プラスとマイナスを全て入れ替える!
と丸暗記しましょう!例えば、
\[\tan(\alpha-\beta)=\displaystyle\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\]
とするだけです。



因みにsin・cosの加法定理の語呂合わせは色々あります。
言葉は悪いんですけど…
「しんだ校長、校長しんだ」・「校長校長、しんだしんだ」
とか、
「しねころす、ころすしね」・「ころすころす、しねしね」
なんかも有名です(笑)どれでもお好きなのでどうぞ。
2倍角の公式 絶対に丸暗記!



一応導いておく?(笑)
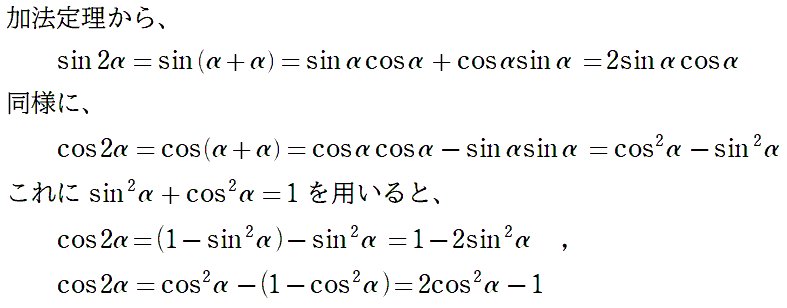
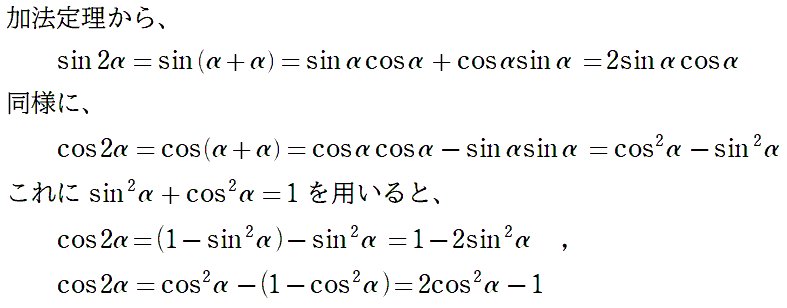
2倍角の公式
\[\begin{split}\sin2\alpha&=2\sin\alpha\cos\alpha\\\cos2\alpha&=\cos^2\alpha-\sin^2\alpha\\&=1-2\sin^2\alpha\\&=2\cos^2\alpha-1\end{split}\]
↑は絶対に全て丸暗記です!例えば、
\(5\sin x+\cos2x<3\)
↓
\(\cos2x=1-2\sin^2x\) 使えば \(\sin x\) の2次不等式だ~



って瞬時に気づけないようではお話になりませんので。
半角公式 絶対に絶対に絶対に丸暗記!



義務感から一応導きます(笑)
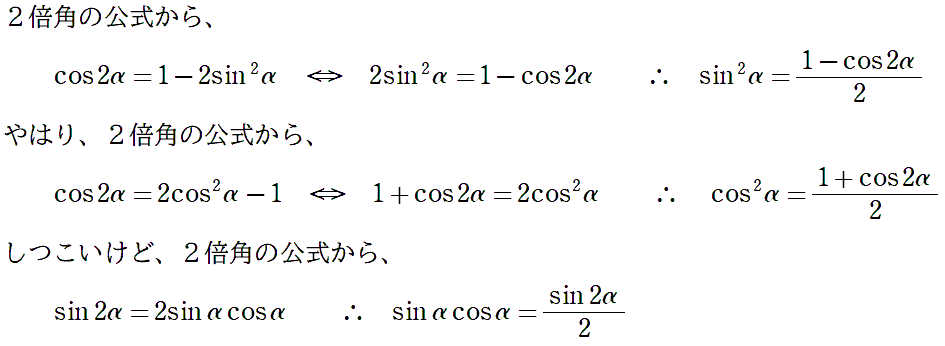
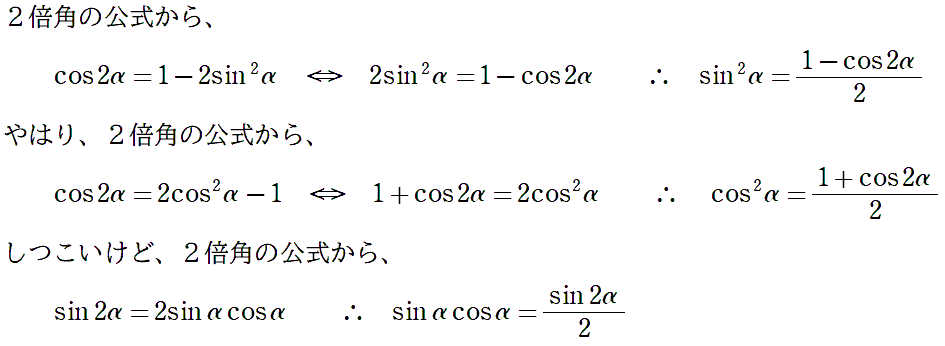
半角公式
\[\begin{split}&\sin^2\alpha=\displaystyle\frac{1-\cos2\alpha}{2}\\&\cos^2\alpha=\displaystyle\frac{1+\cos2\alpha}{2}\\&\sin\alpha\cos\alpha=\displaystyle\frac{\sin2\alpha}{2}\end{split}\]
三角関数の、
左辺は2次式 → 右辺は1次式
と次数を下げられるので、最重要の公式!
です。3式目は2倍角の公式から瞬時に導ける(とゆ~かほぼ同じ)ので、丸暗記するまでもないですが、上2式は丸暗記です!



っつ~か暗記してないなら数学使って受験しちゃダメ(笑)
上2式は形も似ているので、覚えにくいものでもないでしょう。
2倍角の公式からすぐ導けるから丸暗記する必要ないじゃん…
って思ってる人は甘すぎる!
| 半角公式を丸暗記すべき理由 | |
|---|---|
| 文理共通範囲 | 超頻出の 〇\(\sin^2x+\)△\(\sin x\cos x+\)▢\(\cos^2x\) の形の方程式・不等式、最大・最小では半角公式3つを全て使うから! |
| 理系専用範囲 | 超頻出の \(\displaystyle\int\sin^{偶数}xdx\) や \(\displaystyle\int\cos^{偶数}xdx\) の計算では、半角公式を複数回使うことも多い。一問でこれらを何回か計算することもあるので、5回以上使うケースもめずらしくない! |
こんな超頻出問題1問で何回も使うものを丸暗記してないようでは、受験ではお話になりません!



因みにこれらの超有名問題をクッソ時短するテクニックとかもめぐろ塾↓では授業するんだけど、記事が長くなりすぎるから興味がある人は入塾をご検討ください(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
3倍角の公式 丸暗記が、できる人の普通
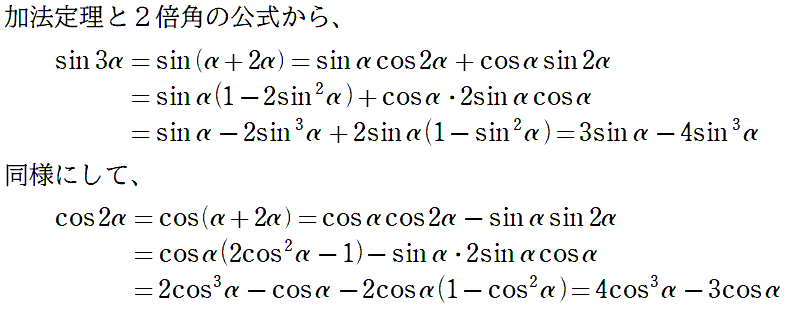
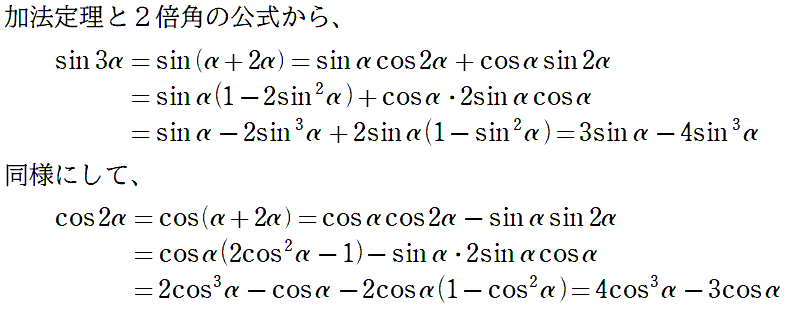
3倍角の公式
\(\sin3\alpha=\:\)\(3\:\)\(\sin\:\)\(\alpha\:\)\(-\:\)\(4\:\)\(\sin\)\(^3\)\(\:\alpha\)
サンシャインひいて夜風が身にしみる
\(\cos3\alpha=\:\)\(4\:\)\(\cos\)\(^3\)\(\:\alpha\:\)\(-\:\)\(3\:\)\(\cos\:\)\(\alpha\:\)
ヨウコさん、さあこすりましょう
↑のような有名な語呂合わせもあるので、偏差値70超えてる人はフツー暗記していると思います。



この記事を見てる男ども…変な想像するなよ…
こっち↓の「こする」だっ!!


2023京大理系数学6(1)は3倍角の公式を暗記してれば瞬時に片付きますし…cos36°の導出でも使う↓


ので、丸暗記を推奨します。
和積・積和公式 絶対に覚えちゃダメ!加法定理から導け!



僕のような凡人は、これらを丸暗記はできません!導け!
導出法
同じ種類の加法定理を書き並べてみましょう。ここではcosの加法定理を使います。
\[\begin{split}\cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\\cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\end{split}\]



右辺が似てるよね?だから足してみると…
\[\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta\]
三角関数の和と積の式が得られます。これを、
- 左→右、つまり和→積に使うのを「和積公式」
- 右→左、つまり積→和に使うのを「積和公式」
と呼ぶだけです。



ここで1つだけ暗記!「積和公式」は上を2で割るだけだけど、「和積公式」で使うときに \(\alpha\;,\;\beta\) を解析するのは面倒です。
「和積公式」で使うときは、\(\left\{\begin{array}{1}\alpha+\beta=A\\\alpha-\beta=B\end{array}\right.\) とおく
↓
足し引きで、\(\left\{\begin{array}{1}2\alpha=A+B\\2\beta=A-B\end{array}\right.\)
↓
\(\alpha=\displaystyle\frac{A+B}{2}\;,\;\beta=\displaystyle\frac{A-B}{2}\) となる
ことだけは暗記!導出のスピードが格段に上がります。以上でcosの加法定理を足したバージョンの和積公式の出来上がり↓
\[\cos A+\cos B=2\cos\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\]
和積・積和公式



前項より、
①sinの加法定理を足す、②引く
③cosの加法定理を足す、④引く
で公式としてまとめると↓のようになります。
和積公式
\(①\;\;\sin A+\sin B\)\(\;=2\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)
\(②\;\;\sin A-\sin B\)\(\;=2\cos\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\)
\(③\;\;\cos A+\cos B\)\(\;=2\cos\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)
\(④\;\;\cos A-\cos B\)\(\;=-2\sin\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\)
積和公式
\(①\;\;\sin\alpha\cos\beta\)\(\;=\displaystyle\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}\)
\(②\;\;\cos\alpha\sin\beta\)\(\;=\displaystyle\frac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}\)
\(③\;\;\cos\alpha\cos\beta\)\(\;=\displaystyle\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}\)
\(④\;\;\sin\alpha\sin\beta\)\(\;=-\displaystyle\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}\)
積和の①と②は「sin〇cos△を和・差に変換したい」ケースで用いることになり、どっち使っても一緒です。



①の \(\alpha\) と \(\beta\) を逆にすれば②になるので、分けて覚えておく必要ゼロ!この8つを「丸暗記しろ!」って言った僕の高校の先生マジで意味不明(笑)
8つ丸暗記できる天才さんはどうぞ暗記してください。でも、凡人ならば、これらは加法定理から導きましょう!
和積公式の使用条件
「積和公式」に使用条件はありません。
| 「積和公式」を導くとき | |
|---|---|
| sin〇cos△を和・差に変換したい | sinの加法定理を足す |
| sin〇sin△を和・差に変換したい | cosの加法定理を引く |
| cos〇cos△を和・差に変換したい | cosの加法定理を足す |



でも例えば、sin〇+cos△を積に変換したいとき…
\[\begin{split}\sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\\cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\end{split}\]
違う種類の加法定理の右辺は似てないから、
足したり引いたりしても意味ない!
↓
和積公式は同種じゃないと使えない!
という使用条件があります。
これを解決してくれるのが、余角公式
です。



\(\displaystyle\frac{\pi}{2}=90^{\circ}\) から元の角度を引けば、sinとcosは変え放題!を使って、こ~しちゃえばオッケー↓





↑ではsinにそろえましたが、cosにそろえてもオッケーです。方程式を解くとき等に使いますが、最終的な解は一致します。
和積・積和公式のまとめ
- 同じ種類の加法定理は似てるから、和・差をとると三角関数の和・差と積の関係式を出せる
- \(\left\{\begin{array}{1}\alpha+\beta=A\\\alpha-\beta=B\end{array}\right.\) とおくと \(\alpha=\displaystyle\frac{A+B}{2}\;,\;\beta=\displaystyle\frac{A-B}{2}\) となることは暗記!
- sin〇±cos△を積に変換するときは、余角公式で種類をそろえておく
因みに使用ケースとしては…
| 和積・積和公式の代表的な使用ケース | |
|---|---|
| 文理共通範囲 | 方程式 sin〇±sin△±…=0 や cos〇±cos△±…=0 を解くときに和積公式を利用。 |
| 理系専用範囲 | sinとcosの1次式の和・差の積分で積和公式を利用。 |
となりますが…そこまで頻出とは言えないので…



使えなくも大学受験は何とかなるかも(笑)
でも加法定理さえ丸暗記していればカンタンに導けるから、おさえとかないのはもったいないです!
合成公式 sinへの合成だけは丸暗記!
sinへの合成(手順を丸暗記!)



例として、
\(\sin x-\sqrt{3}\cos x\) を1つのsinに
まとめてみます。
この手順を丸暗記してください。
(sinの係数は \(x\) 座標に、cosの係数は \(y\) 座標に)
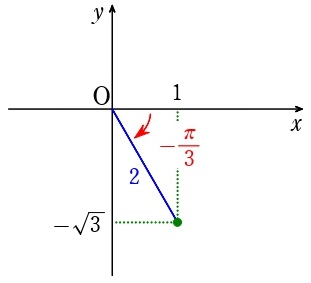

\(\sin x-\sqrt{3}\cos x=\;\)\(2\)\(\sin(x\)\(-\displaystyle\frac{\pi}{3}\)\()\)



sinへの合成は、以下の文理共通範囲の超頻出問題↓
| 問題の形 | 解法 |
|---|---|
| \(a\sin〇±b\cos△\) の形の方程式・不等式、最大・最小 | 基本、sinへの合成 |
| 〇\(\sin^2x+\)△\(\sin x\cos x+\)▢\(\cos^2x\) の形の方程式・不等式、最大・最小 | 半角公式を使って、sinへの合成 |
| sinとcosの対称式 | \(\sin x+\cos x=t\) とおいて、最終的に、または \(t\) の変域を調べるのに、sinへの合成 |
で使うので手順を丸暗記し、作業化しておく必要があります!
合成の意味
2021共通テスト等で、sinへの合成の意味を理解した上でのcosへの合成が問われました。



GMARCHの文系学部のどっか(詳細は忘れたw)も2020周辺で出題してましたね。sinへの合成の頻度に比べれば1/100くらいの出題頻度ですが(笑)
加法定理を \(r\) 倍し、逆利用しています。
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
↓ \(r\) 倍し、逆に書く
\(r\cos\beta\;\)\(\sin\alpha+\)\(r\sin\beta\;\)\(\cos\alpha=\;\)\(r\;\)\(\sin(\alpha\)\(+\beta\)\()\)
↓
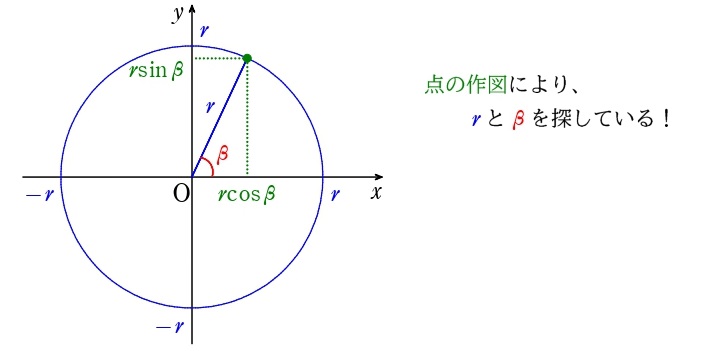




にすぎないんですよね…これさえ理解していれば…
cosへの合成



先ほどの \(\sin x-\sqrt{3}\cos x\) を1つのcosにまとめてみましょう。
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
↓ \(r\) 倍し、逆に書く
\(r\sin\beta\;\)\(\sin\alpha+\)\(r\cos\beta\;\)\(\cos\alpha=\;\)\(r\;\)\(\cos(\alpha\)\(-\beta\)\()\)
(sinの係数は \(y\) 座標に、cosの係数は \(x\) 座標に)
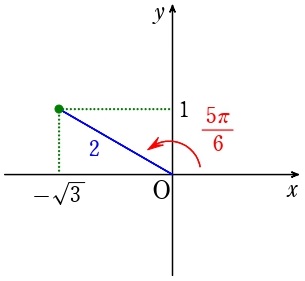

\(\sin x-\sqrt{3}\cos x=\;\)\(2\)\(\cos(x\)\(-\displaystyle\frac{5\pi}{6}\)\()\)
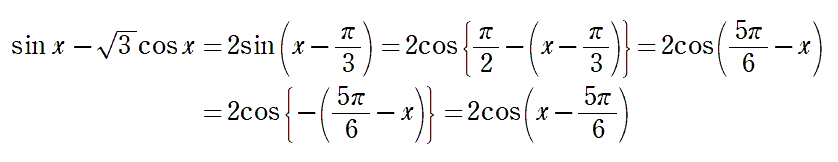
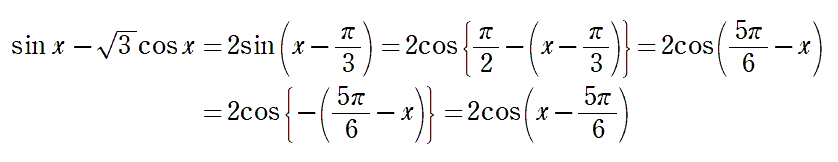
まとめ



丸暗記すべき「三角関数の公式」は…
定義・余角公式・加法定理・2倍角の公式・半角公式・3倍角の公式・sinへの合成
だけです。



後は覚えんで良し!導け!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








