「微分の定義式」って覚えるの?

 めぐろ塾の安田
めぐろ塾の安田何回も導きすぎて形まで覚えちゃうってのが正解
微分の目的から「導関数の定義式」を導いてみよう
教科書では「微分係数」から説明されますが、ここでは分かりやすさ重視で「導関数」からいきましょう!
微分の目的



これは必ず暗記してください!
微分の目的は、接線の傾きを求めること!
この目的から、定義式は自分で導出できるようにしておくことが大切です。
「導関数の定義式」の導出
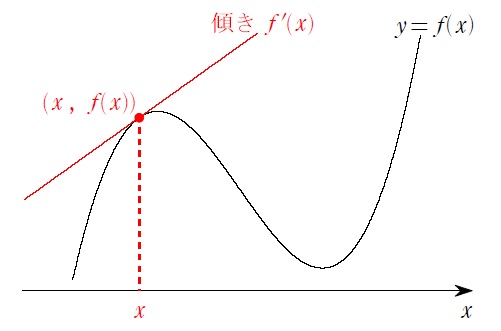




赤の接線の傾きを求めるのが目的で、これが導関数 \(f'(x)\) と言われるものです。
直線の傾きを決めるためには2点が必要ですが、今は \((x\:,\:f(x))\) という1点しか分かっていません。な~んも関係ないとこにもう1点をとってもしょうがないので、グラフ上の \(x\) 座標が \(h\) だけ進んだところにもう1点をとって傾きを求めることにしましょう。
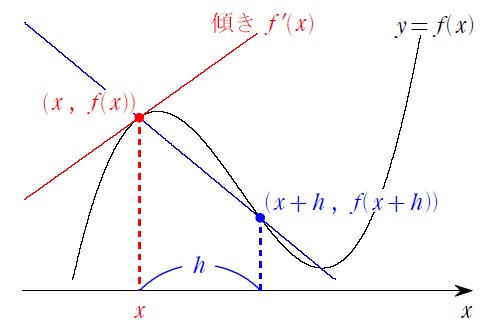

この青の直線の傾きは、 \(\displaystyle\frac{f(x+h)-f(x)}{h}\) となり、\(y=f(x)\) の \(x\) から \(x+h\) までの「平均変化率」と呼ばれます。



「平均変化率」ってのも2015センター試験ⅡBで問われてるから、一応覚えておくのがベスト!
この青の直線の傾き=「平均変化率」は、↑の状態では目的の赤の直線の傾き \(f'(x)\) とは全く異なりますが…
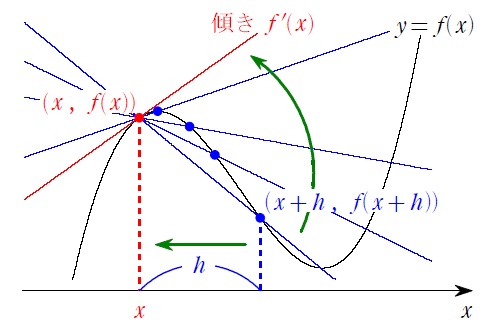

\(h\) を小さくしていけば、目的の赤の直線の傾き \(f'(x)\) に近づいていく
ことが分かります。



文系の人はほとんど扱わないんだけど、この「近づける」ってための記号が「\(\lim\)(極限)」ってもので…「導関数の定義式」の完成↓
導関数の定義式
\(f'(x)=\:\)\(\displaystyle\lim_{h\to0}\:\)\(\displaystyle\frac{f(x+h)-f(x)}{h}\)
冒頭で言った通り、上のように
グラフ上に2点をとって、近づける
って流れで「何回も導きすぎて形まで覚えちゃう」ってのが正解です!
「導関数」と「微分係数」の違い



教科書では「微分係数の定義式」は、さっき作った「導関数の定義式」の \(x\) を \(a\) に変えた形で紹介されるよね。
微分係数の定義式(教科書バージョン)
\(f'(a)=\:\)\(\displaystyle\lim_{h\to0}\:\)\(\displaystyle\frac{f(a+h)-f(a)}{h}\)
\(a\) になってるから混乱してる人が多いんだけど…この \(a\) は例えば \(a=7\) って具体値って意味!だから…
- 導関数
\(x=1\) でも \(x=\sqrt{2}\) でも \(x=\pi\) でも…どこでもオッケーなもの - 微分係数
例えば \(x=7\) に限定した…ピンポイントでのお話
「微分係数の定義式(実用的バージョン)」の導出



問題文で \(h\) なんてあんま登場しないでしょ(笑)登場するのは \(x\) !
だから「微分係数の定義式」は \(x\) を使った形でおさえておいた方が良い!これをこの記事では「実用的バージョン」と呼ぶことにします(笑)やはり、
グラフ上に2点をとって、近づける
って流れで自分で導けるようにしましょう!君らが混乱しないように、ここでは \(y=f(x)\) の \(x=7\) の微分係数 \(f'(7)\) を導きますが、\(x=3\) なら下の流れの \(7\) を \(3\) に変えるだけ~。
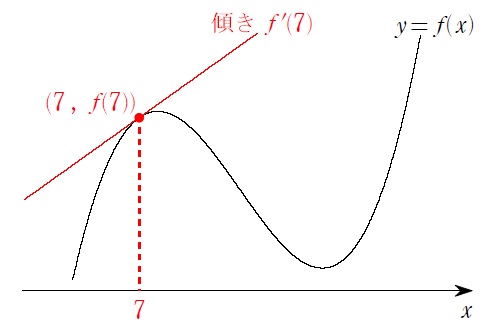

赤の直線の傾き \(f'(7)\) を求めるのが目的です。「導関数」ではここが \(x\) だったので \(h\) を使いましたが、グラフ上のもう1点の \(x\) 座標に \(x\) を使うことができます。
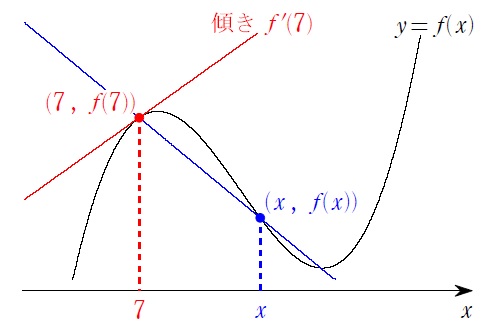

今回、この青の直線の傾き=「平均変化率」は、 \(\displaystyle\frac{f(x)-f(7)}{x-7}\) です。後は今回は \(h\) を使ってないことを意識すれば…この傾きは…
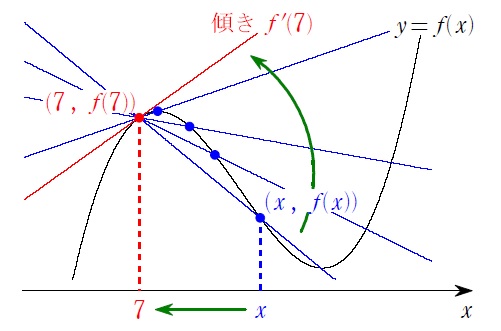

\(x\) を \(7\) に近づければ、目的の赤の直線の傾き \(f'(7)\) に近づいていく



ので、「微分係数の定義式(実用的バージョン)」の完成↓
微分係数の定義式(実用的バージョン、\(x=7\) のとき)
\(f'(7)=\:\)\(\displaystyle\lim_{x\to7}\:\)\(\displaystyle\frac{f(x)-f(7)}{x-7}\)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
導けるようにしておかなきゃダメ?
導けなくてもぶっちゃけそこまで困らないけど…
「導関数の定義式」から \(f(x)=x^2\) の導関数を導くと…
\[\begin{split}f'(x)&=\displaystyle\lim_{h\to0}\displaystyle\frac{f(x+h)-f(x)}{h}\\&=\displaystyle\lim_{h\to0}\displaystyle\frac{(x+h)^2-x^2}{h}\\&=\displaystyle\lim_{h\to0}\displaystyle\frac{2xh+h^2}{h}\\&=\displaystyle\lim_{h\to0}(2x+h)=2x\end{split}\]
ってなりますが…



受験での微分計算は公式でやっちゃうからね~(笑)
\(f(x)=x^2\) なら、「肩を下ろして、次数を1つ下げる」って公式があるんで、これで \(f'(x)=\:\)\(2\:\)\(x\:\)\(^{2-1}\:\)\(=2x\) って計算しちゃいます。従って…



ぶっちゃけ「微分の定義式」が導けなくてもそこまでは困らない(笑)
恥ずかしながら、現役で早稲田理工の僕、受験時はビミョーでしたm(_ _)mでも…
微分公式の証明が出題されることもあるし…
ちょうど2023慶應理工の問題1(1)で出題されています。
これ系の問題はアウト
「微分の定義式」を「何回も導きすぎて形まで覚えちゃうのが正解」ってのは、上位校で頻出な次のような系統の問題のためです。
2019東大第5問



一部を簡略化して抜粋します。最終的に以下の計算が必要でした。
\[\displaystyle\lim_{x\to1}\displaystyle\frac{\sqrt{x\cos x}-\sqrt{\cos 1}}{x-1}\]



これは「極限計算」の知識ではどーやっても解けません。「微分係数の定義式(実用的バージョン)」を逆に利用して、微分計算に持ち込みます。
\(f(x)=\sqrt{x\cos x}\) とすると、
\(\displaystyle\lim_{x\to1}\displaystyle\frac{\sqrt{x\cos x}-\sqrt{\cos 1}}{x-1}=\:\)\(\displaystyle\lim_{x\to1}\displaystyle\frac{\sqrt{x\cos x}-\sqrt{1\cdot\cos 1}}{x-1}=f'(1)\)
ここで、 \(f'(x)=\displaystyle\frac{\cos x-x\sin x}{2\sqrt{x\cos x}}\) であるから、
\(\displaystyle\lim_{x\to1}\displaystyle\frac{\sqrt{x\cos x}-\sqrt{\cos 1}}{x-1}=f'(1)=\displaystyle\frac{\cos 1-\sin 1}{2\sqrt{\cos 1}}\) (答)
まとめ
2019東大第5問のような問題に備えて、



他にも「微分可能性」の問題とかでも必須なんだけど、この記事では割愛(笑)
「微分の定義式」は、
グラフ上に2点をとって、近づける
って流れで「何回も導きすぎて形まで覚えちゃう」ようにしましょう!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








