「ｎ角形の内角の和」なんて…覚えちゃダメ！
大学受験数学で覚えて欲しいことは、他にもっとたくさんあります。
めぐろ塾の安田因みにここでは、度数法と弧度法の両方を使います！
弧度法を良く知らない人、\(180^\circ=\pi\) ってだけ
覚えるならこの言葉。
めぐろ塾の安田多角形でたら、三角形で何とかしろ！
結論：多角形は、三角形に分割しよう！
教科書でも数学Ⅰで「三角比」ってテーマがあって、ここで三角形について色々勉強させられます。
めぐろ塾の安田でも高校の教科書に「多角形」ってテーマはないんだよ
何でかってゆーと、多角形は三角形で何とかできちゃうから。
五角形を例に考えてみよう！
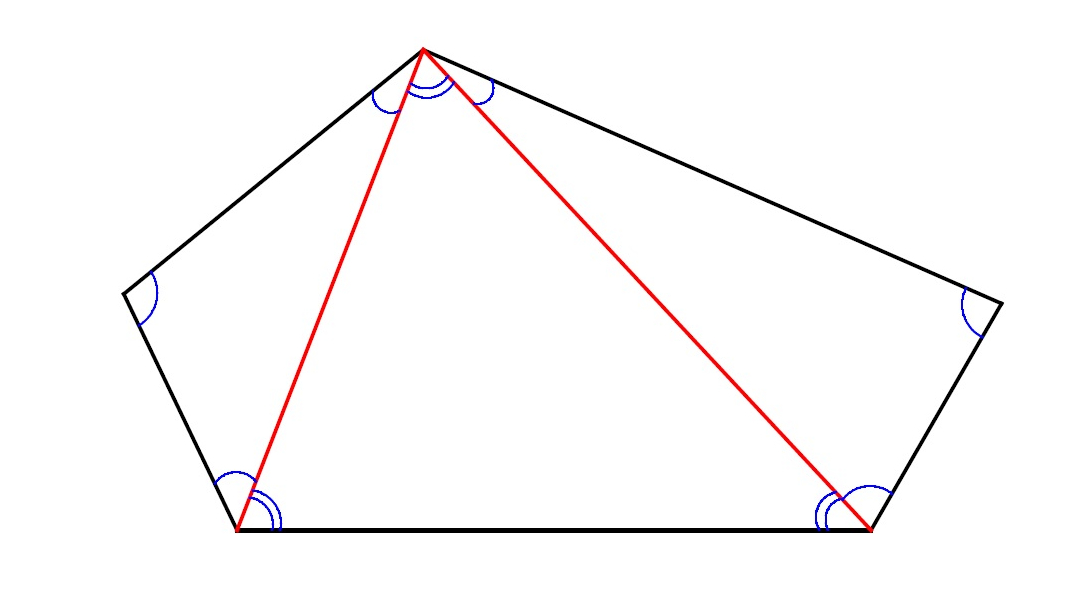
黒を辺とする五角形があるけど、赤い対角線２本で三角形３つに分割できるよね。
めぐろ塾の安田この３つの三角形の内角の和って、五角形の内角の和になってない？
だから、
（五角形の内角の和）＝（三角形の内角の和）×３ \(=3\pi=540^\circ\)
めぐろ塾の安田（三角形の内角の和）\(=180^\circ=\pi\)
は流石に知ってるよな？信じてるぞ(笑)
ｎ角形に拡張すると…
ｎ角形でも同じように考えるだけ。
下の黒を辺とするｎ角形を考えてみましょう。
めぐろ塾の安田頂点に１～ｎって番号つけておくね
頂点ｎからは、頂点２～ｎー２までにｎー３本の対角線を引くことができます。
このｎー３本をすき間とする、ｎー２個の三角形の内角の和が、ｎ角形の内角の和です。
めぐろ塾の安田頂点ｎから頂点１～ｎー１に引いたｎー１本の線のすき間にｎー２個の三角形ができる、って考えてもオッケー
だから、
ｎ角形の内角の和
（三角形の内角の和）×（ｎー２）\(=(n-2)\times180^\circ=(n-2)\pi\)
めぐろ塾の安田凸多角形として導きましたが、凹多角形の場合も結果は同じです。この言葉の意味が分からない人は気にしなくてオッケー(笑)
忘れちゃっても…
繰り返すけど、こんな簡単に出せるものを覚えちゃダメです！
めぐろ塾の安田ま～何度もやってると覚えちゃうんだけど(笑)
覚えるにしても、
めぐろ塾の安田確かｎ角形の内角の和って、\((n-？)\pi\) っぽくなかったっけ？
でオッケー。上の公式は \(n ≧ 2\) で成立します。
二角形なんて作れないから、内角の和＝０にしなきゃ
でもいいし、
三角形の内角の和＝\(\pi\) にしなきゃ
って思えば、？が２となることくらい出せるから。
大学受験数学で定石の三角形分割
「本質を理解しなきゃダメだ！」
めぐろ塾の安田なんてカッコいいこと言うつもりはない
「ｎ角形の内角の和」は \((n-2)\pi\) を覚えるってことよりも、それを導くのに使う、多角形は三角形で考えるって意識の方が大学受験数学では点数になるんです。
いくつか例を挙げましょう。
二等辺三角形
問題
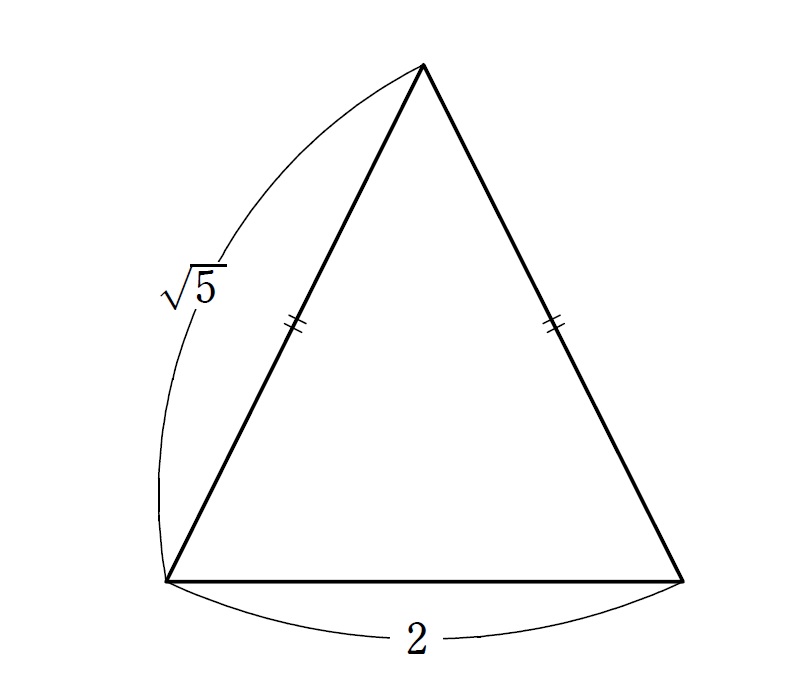
下の二等辺三角形の面積を求めよ。
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
解説
めぐろ塾の安田暗算できましたか？
授業でこの面積計算が必要な問題（内接円の周の長さの無限級数）をやらすと…
- 余弦定理を使ってから、\(\displaystyle\frac{1}{2}\times\) (２辺の長さの積) \(\times\sin\)(挟角) で計算する
- ヘロンの公式を使う
生徒が結構いるんですよね。
めぐろ塾の安田ヘロンの公式を使われると…優秀なのかバカなのか分からなくなる(笑)
これが一番簡単↓
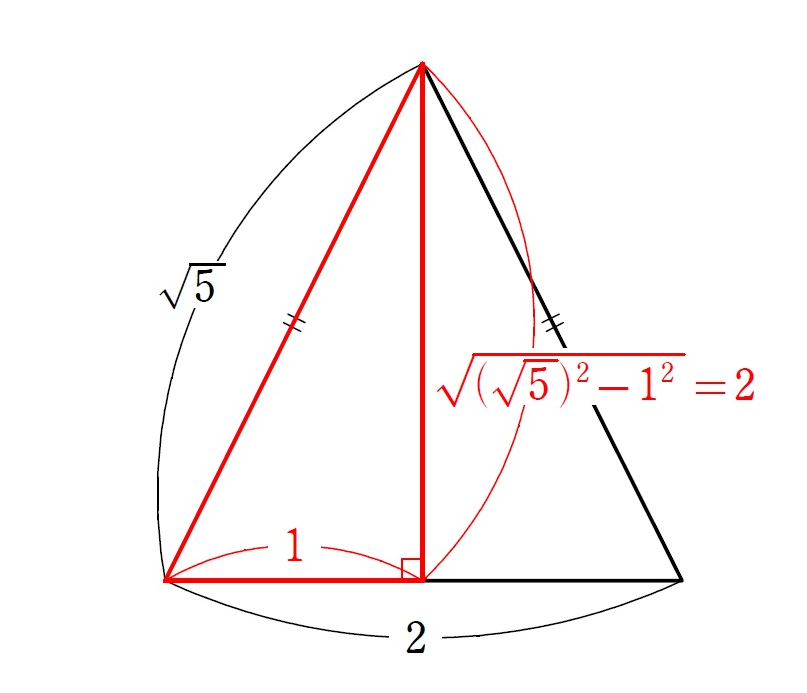
このように、半分に割って直角三角形を作り、三平方の定理で高さを２と計算してしまえば、面積は、
\(\displaystyle\frac{1}{2}\times2\times2=2\) （答）
というように、ほぼ暗算できてしまいます。
半分に割って、直角三角形を作る
めぐろ塾の安田二等辺三角形を見たら即座に半分に割るクセをつけておくこと
極めて簡単な問題を例にしましたが、
- 二等辺三角形の内接円の半径の漸化式を立式するとき
- 直円錐が関連する体積の最大最小問題
- 円に内接するｎ角形の問題
といった、そこそこ応用的な問題でも使います。
円に内接する四角形
センター試験ⅠＡでは頻出の内容でした。
ここで紹介する内容は、2022年度までの共通テストⅠＡの本試では出題されていませんが、それ以外では頻出です。
めぐろ塾の安田ここでは最低２つの言葉、できれば「トレミーの定理」も覚えて！
対角の和が \(\pi=180^\circ\)
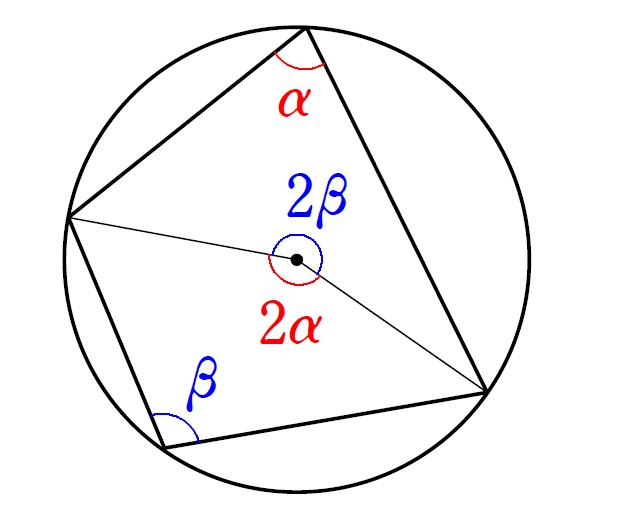
太線で円と、それに内接する四角形を書いておきました。
めぐろ塾の安田中心角は、円周角の２倍
なので、上図の中心角に注目することで、
\(2\alpha+2\beta=360^\circ\) ∴ \(\alpha+\beta=180^\circ=\pi\)
対角線で三角形に分割
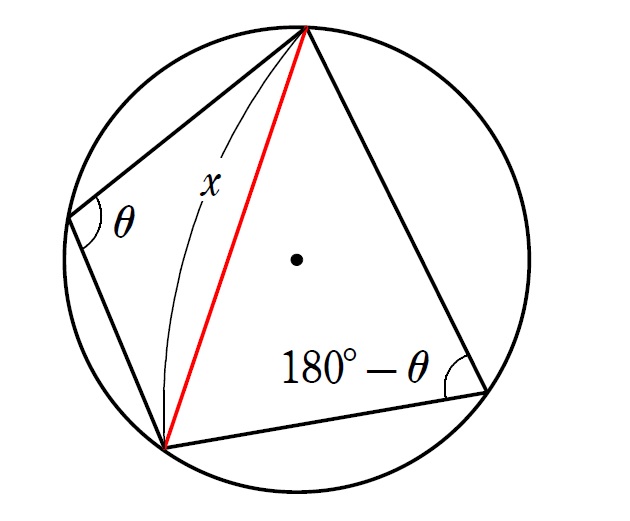
対角線で三角形２つに分割し、正弦・余弦定理を利用しましょう。
対角線の引き方は２通りありますが、大体は問題文で「～の角度を \(120^\circ\) とする」とか「～の長さを求めよ」といった、
めぐろ塾の安田「こっちに対角線引いてくださいね～」的な誘導がつく。
４辺の長さが与えられたとき、上のように \(x\:,\:\theta\) を設定して、余弦定理２回で \(x\) と \(\cos\theta\) の連立方程式を導き、対角線の長さ \(x\) を求める問題は超有名です。
- 対角の和が \(\pi=180^\circ\)
- 対角線で三角形２つに分割し、正弦・余弦定理
を利用する
トレミーの定理
円に内接する四角形の問題では、上の２つが実行できればほぼほぼ困りません。
でも…
対角線って２つ引けるんでしょ？
両方の長さ求めろって言われたら結構だるくね？
って思った人もいるんじゃない？
そこで活躍するのが「トレミーの定理」です。
証明問題が大学受験で出題されてるの見たことないから、言葉で結果だけ。
トレミーの定理
円に内接する四角形では、
（対角線の長さの積）＝（対辺の長さの積の和）
が成立する
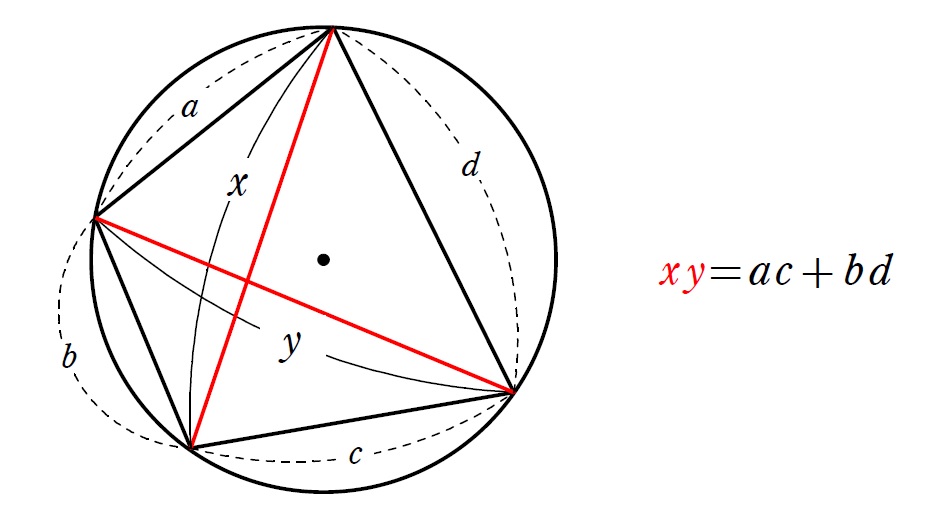
「トレミーの定理」が受験で最も効力を発揮するのは、正五角形の対角線計算なんですが、これについては次項の内容も絡めて、２つ後の記事↓で扱います。
正五角形
めぐろ塾の安田正五角形に対角線を引いて、角度 \(\displaystyle\frac{\pi}{5}=36^\circ\) を●として書き込むと下図のようになるよ
どの三角形に注目しても、内角で「●が５つ分」\(=\pi=180^\circ\) になっていることが分かります。
めぐろ塾の安田「数学は美しい」って言葉はキライなんだけど、これは美しいね(笑)
正五角形の中に登場する角度は \(\displaystyle\frac{\pi}{5}=36^\circ\)（とその２倍 \(72^\circ\) 、３倍 \(108^\circ\)）ばっかりってことは暗記しといた方がいいんだけど…
大学受験で必要なとこだけ証明
五角形の内角の和は \((5-2)\times180^\circ=540^\circ\) だから、正五角形の内角は、
\[\displaystyle\frac{540^\circ}{5}=108^\circ\]
● \(=\displaystyle\frac{180^\circ-108^\circ}{2}=36^\circ\)
\(\alpha\) \(=108^\circ-\) ●\(\times2=108^\circ-72^\circ=\) \(36^\circ=\) ●
\(\beta\) \(=180^\circ-\) ●\(\times3=180^\circ-108^\circ=72^\circ=\) ●\(\times2\)
これで上図の赤い三角形も二等辺三角形であることが証明できました。
一辺の長さが１の正五角形の対角線の長さを求めてみよう！
めぐろ塾の安田ここまで詳しく説明したら余裕でしょ！二等辺三角形の相似を利用します。
対角線の長さを \(l\) とすると、二等辺と対称性から、下図のように辺の長さが求まります。
角度マークから分かる通り、青の三角形∽赤の三角形なので、底辺斜辺比を考えれば、
\(1:l\) ＝ \((l-1):1\)
\[\Leftrightarrow\:\:l(l-1)=1\:\:\Leftrightarrow\:\:l^2-l-1=0\]
\(l>0\) より、解の公式から、\[l=\displaystyle\frac{1+\sqrt{5}}{2}\]
めぐろ塾の安田因みに、\(1:l\) は黄金比と呼ばれ、大学受験で超頻出！
ここまでの流れを理解した上で、一辺の長さ１の正五角形の対角線の長さとして値を暗記しておくのがオススメです。
対角線を引いてできる「頂角が \(36^\circ\) の二等辺三角形」の相似を利用
することで、
（一辺の長さ１の正五角形の対角線の長さ）＝ \(\displaystyle\frac{1+\sqrt{5}}{2}\)
円に内接するｎ角形
大学受験では正ｎ角形で出題されることがほとんどなので、正ｎ角形メインで扱います。
問題
\(n\) を \(3\) 以上の自然数とする。半径 \(1\) の円に内接する正 \(n\) 角形の一辺の長さを求めよ。
↓
↓
↓
↓
↓
↓
↓
↓
解説
めぐろ塾の安田すぐに下の図を描けた人はオッケー！描けなかった人、2019の早稲田理工の第２問とかアウトになっちゃう
この図さえ描けてしまえば、求める一辺の長さは黒の線分の長さで、線分マーク「〇」の２つ分です。
図中の斜角 \(\displaystyle\frac{\pi}{n}\) の直角三角形に注目することで「〇」＝ \(\sin\displaystyle\frac{\pi}{n}\) が分かるので、
（半径 \(1\) の円に内接する正 \(n\) 角形の一辺の長さ）＝ \(2\sin\displaystyle\frac{\pi}{n}\) （答）
めぐろ塾の安田直角三角形では、斜辺に「\(\sin\)(斜角)」をかけると高さ、斜辺に「\(\cos\)(斜角)」をかけると底辺の長さが求まるよ！
何でその図を描くの？
めぐろ塾の安田暗記
って言いたいとこだけど、ちゃんと動機も説明するね。
因みに2019の早稲田理工では、「正ｎ角形」って言われてるだけで、「円に内接する」とは言われていません。
めぐろ塾の安田「正ｎ角形は、当たり前に円に内接する」ってことはおさえといてね！
「円に内接するｎ角形」の場合は、
- 二等辺三角形を作りたい！
- 円の半径を使いたい！
ってゆー動機から、対角線ではなく、中心をターゲットにして二等辺三角形を作ります。
に分割できるので、
めぐろ塾の安田正ｎ角形は、ｎ個の二等辺三角形に分割されるに決まってる！
後は簡単でしょう。
ｎが大きいと二等辺三角形は凄く細くなるわけですが、
- 見易さ重視で、あまり細く描きすぎないこと
- 図に情報量が多いと混乱するので、たくさん描かないこと
も意識してください。
今回の場合、二等辺三角形は１つ描くだけで十分です。
因みに、上図の青い線分は「正ｎ角形の内接円の半径」になります。
めぐろ塾の安田この図から、内接円の半径は \(\cos\displaystyle\frac{\pi}{n}\) って分かるよね。
これを考えさせる問題も、大学受験では頻出！
- 円の中心を頂角とする二等辺三角形を作成
- 頂角の和が \(2\pi=360^\circ\)
を利用する
ちょっと応用的な話。正ｎ角形じゃない場合は…
上の赤枠について、
「頂角が \(\displaystyle\frac{2\pi}{n}\)」で良くね？
って思った人もいるんじゃない？
めぐろ塾の安田正ｎ角形の場合はそれでも大丈夫。でも…
ただの「ｎ角形」の場合はダメ。
頂角が等差数列で増えていく問題も1999の高知医科大で出題されています。
めぐろ塾の安田だから「頂角の和が \(2\pi=360^\circ\)」っておさえといた方がいい。
因みに、円に内接するただの「ｎ角形」の場合、円の中心がｎ角形の外部にくることもある…
一例として、1999の岡山大の複素数の問題の解答の一部を↓
太線で描かれた「円に内接する五角形」の面積を求めていますが、円の中心が五角形の外にあります。
めぐろ塾の安田この場合は、「頂角の和が \(2\pi=360^\circ\)」も使えない…残念(笑)
でも上の解答を見ても分かる通り、円の中心を頂角とする二等辺三角形を作ることが大切なのは変わりません。
まとめ
いろいろ長ったらしく説明してきましたが、結局大事なのはこの言葉。
めぐろ塾の安田多角形でたら、三角形で何とかしろ！
今回も長くなっちゃってごめんねm(_ _)m
君の大学受験が最高の結果になることを祈ってます！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
