【大学受験】数学の公式は、絡めて覚えれば忘れない！
大学受験の数学で使う公式って…
多すぎて…覚えてもすぐに忘れちゃう…
めぐろ塾の安田そんな君の悩みを少しだけ解決してあげよう！！
…あくまで…「少しだけ」…(笑)
正しい「数学の公式」の覚え方
導出から深く理解する
チョー王道の覚え方ですね。学校の先生の多くは、公式が登場したときに導出や証明を丁寧に説明するんじゃないでしょうか？
めぐろ塾の安田これは君たちに深く理解してもらって、忘れないようにするため！
…ま～「証明はやっとかないと」ってゆー教える側の義務感みたいなのも当然ありますが…(笑)
でもね～…「ヘッセの公式」とかは一般証明スゲー面倒な割に受験で証明はあんま出ないし…
ってゆー、導出まで理解しようとするとコスパ悪い公式もあるんですよ…
めぐろ塾の安田僕はこーゆーのは証明をプリントに載っけるだけで、授業時間内で導出は扱いません
何度も使う
めぐろ塾の安田これ読んでる人の中で、「２次方程式の解の公式」を忘れてる人はいないよね？(笑)
なぜ受験生のほぼ全てが「２次方程式の解の公式」を忘れないのか？
日常的に数学を解いてれば、イヤでも一日数回は使うから。
何度も使えば忘れないから、何度もやる！
これも数学の公式の王道の覚え方です。
めぐろ塾の安田僕はそこそこマイナーな公式でも、もう忘れられない。たとえ痴呆症になっても。…だって…何十回も授業してるから(笑)
でも…教科書に載ってるけど使用頻度の低い公式ってのもあるんですよね…
めぐろ塾の安田例えばこれとか。こーゆーのも真面目におさえようとすると…コスパは悪い…にも関わらず…
上位校はこーゆーのを重箱のスミをつつくように出題してくることもあるから…おさえてないと出題されたときに終わっちゃう…ってゆーことも(笑)
複数の公式を絡めて覚える
めぐろ塾の安田凄く限定的ではあります。でも…
複数の公式を、絡めて覚えておける！
ものもあるので…
めぐろ塾の安田今回の記事ではこの部分にフォーカスして…
複数の公式を絡めた覚え方をいくつか紹介します！！
「三角形の成立条件」と「２円が交わる条件」
三角形の成立条件
三角形の辺の長さが正ってのは当然ですが…
めぐろ塾の安田正でも、例えば１と３と７って辺の長さの三角形は作れない！
から。なので、「一辺＜他の２辺の和」になってる必要があって、これを全ての組み合わせで立式して整理すると…
三角形の成立条件
\(a\:,\:b\:,\:c\) が三角形の３辺の長さとなるための条件は、
\(|b-c|<a<b+c\)
めぐろ塾の安田使用頻度は高くないんですけどね(笑)でも医学部の小問集合とかでたまに出るし、2002一橋の整数問題で使ったりもしました。だから覚えとかないと、って内容
２円が交わる条件
めぐろ塾の安田英語キライな僕でも「distance」＝「距離」は覚えてる、だって数学で使うから(笑)
数学で距離はこの頭文字「\(d\)」って書くことが多いことは意識しましょう。
- 円は図形的考察が有効
- 円の形は半径が、位置は中心が決めている
とかってゆー本質説明は省きます(笑)「２円が異なる２点で交わる」って言われた瞬間に…
って考えて、次の式が立てられないとアウトです。
２円が交わる条件
中心間距離 \(d\) 、半径が \(r_1\:,r_2\) の２円が異なる２点で交わる条件は、
\(|r_1-r_2|<d<r_1+r_2\)
めぐろ塾の安田図では \(r_1>r_2\) ってしてるけど、半径に文字が入って大小判断ができない場合もあるから、内接のときには絶対値が必要です。
形が全く一緒でしょ？
「三角形の成立条件」と「２円が交わる条件」って式の形が全く一緒だよね？これって…
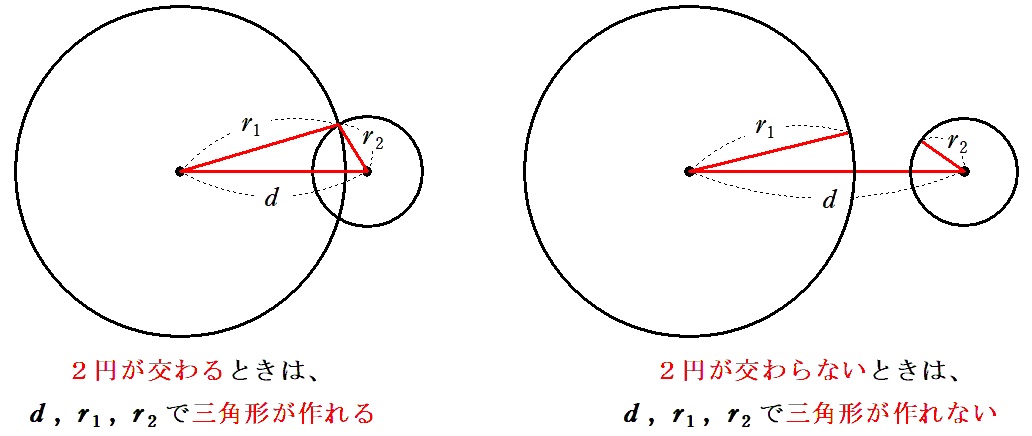
から。「三角形の成立条件」の方が使用頻度低いので、
めぐろ塾の安田って覚えとくのがオススメです！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
「ベクトルのなす角」と「相関係数」
内積の定義式、
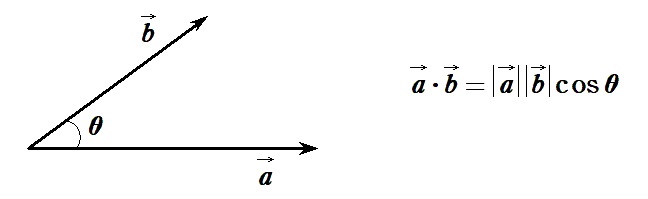
から割り算ですぐに導けますが…
めぐろ塾の安田空間で角度が話題に挙がったら、瞬時に次の式を頭に浮かべて欲しい。
ベクトルのなす角
\(\overrightarrow{a}\) と \(\overrightarrow{b}\) のなす角を \(\theta\) とすると、
\[\cos\theta=\displaystyle\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}\]
ほんで2023共通テストⅠＡでももちろん登場した「相関係数」も紹介しましょう。
めぐろ塾の安田(共分散)＝(偏差積の平均)だと、単位かえると相関かわらないのに値かわっちゃうから、単位キャンセルのために標準偏差の積で割るだけなんだけど…
複雑に式で書くと…
相関係数
２つの変量 \(x\:,\:y\) からなる \(n\) 個のデータ \((x_1\:,\:y_1)\:,\:(x_2\:,\:y_2)\:,\)\(\:\cdots\:,\:(x_n\:,y_n)\) があり、\(x\:,\:y\) の平均値をそれぞれ \(\bar{x}\:,\:\bar{y}\) とすると、変量 \(x\:,\:y\) の相関係数 \(r\) は、
\[\scriptsize{r=}\tiny{\displaystyle\frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\:\cdots\:+(x_n-\bar{x})(y_n-\bar{y})}{\sqrt{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\:\cdots\:+(x_n-\bar{x})^2}{\sqrt{(y_1-\bar{y})^2+\:\cdots\:+(y_n-\bar{y})^2}}}}\]
ちょっと大学内容に入っちゃうんですけどね。\(n\) 個の成分のベクトルでも、
- 大きさは、各成分の２乗の和にルートをつける
- 内積は同じ高さの成分をかけて和をとる
ってゆー成分計算方法は変わりません。だから、\(\overrightarrow{a}=\begin{pmatrix}x_1-\bar{x} \\ x_2-\bar{x} \\ \vdots \\ x_n-\bar{x} \end{pmatrix}\:\:,\:\:\overrightarrow{b}=\begin{pmatrix}y_1-\bar{y} \\ y_2-\bar{y} \\ \vdots \\ y_n-\bar{y} \end{pmatrix}\) として相関係数 \(r\) の式を書き換えると、
\[r=\displaystyle\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}=\cos\theta\]
になっていることが分かります。このことを意識しておくと、
- 相関係数の式で、「分母が標準偏差の積」であることを忘れにくくなる
- 相関係数 \(r=\cos\theta\) だから、\(-1≦r≦1\) が当たり前になる
めぐろ塾の安田ってゆー微々たるメリットがあるよ(笑)
「三角形の面積公式（ベクトル）」と「コーシー・シュワルツの不等式」
三角形の面積公式（ベクトル）
めぐろ塾の安田2023一橋大の３で使ったばかり(笑)
三角形の面積公式（ベクトル）
２つのベクトル \(\overrightarrow{a}\:,\:\overrightarrow{b}\) の作る三角形の面積 \(S\) は、
\[S=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{a}\right|^2\left|\overrightarrow{b}\right|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2}\]
「ベクトルのなす角」からすぐ導けるんですけどね↓
めぐろ塾の安田でも空間で三角形の面積求めるときの大半で使う公式だから、完全暗記しとくべきだと思う。
因みに1／2をなくすと平行四辺形の面積公式にでき、2014東大の理系数学第１問とかはこの公式をおさえてれば瞬殺です。
これのルートの中身≧０が、コーシー・シュワルツの不等式
めぐろ塾の安田ルートの中身≧０って法律あるじゃん？(笑)
「三角形の面積公式（ベクトル）」のルートの中身≧０から、
\[\left|\overrightarrow{a}\right|^2\left|\overrightarrow{b}\right|^2≧\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2\]
これの \(\overrightarrow{a}=\begin{pmatrix}p \\ q \\ r \end{pmatrix}\:\:,\:\:\overrightarrow{b}=\begin{pmatrix}a \\ b \\ c \end{pmatrix}\) ってしてみると、あ～ら不思議…
コーシー・シュワルツの不等式
任意の実数 \(p\:,\:q\:,\:r\:,\:a\:,\:b\:,\:c\) について、
\((p^2+q^2+r^2)(a^2+b^2+c^2)\:\)\(≧(pa+bq+rc)^2\)
が成立し、
等号成立は、\(p:a=q:b=r:c\)
のときである
めぐろ塾の安田のできあがり！出題頻度は低いけど(笑)
ほんでこーゆーの使うときは「等号成立」を調べなきゃいけないって法律あるんだけど(笑)
等号成立条件も、
「三角形の面積公式（ベクトル）」のルートの中身＝０のとき
↓
２つのベクトル \(\overrightarrow{a}\:,\:\overrightarrow{b}\) の作る三角形の面積＝０のとき
↓
\(\overrightarrow{a}/\!/\overrightarrow{b}\) のとき
って感じで、絡めて暗記できます。
「相加相乗平均の不等式」と「等差・等比中項」
相加相乗平均の不等式
３数の場合の証明には \(y=\log x\) のグラフの凸性を使うので、ここでは形だけ↓を紹介します。
相加相乗平均の不等式
\(a>0\:,\:b>0\:,\:c>0\) について、
\(\displaystyle\frac{a+b}{2}\:\)≧\(\:\sqrt{ab}\) 、 \(\displaystyle\frac{a+b+c}{3}\:\)≧\(\:\sqrt[3]{abc}\)
が成立し、
等号成立は、\(a=b=c\)
のときである
めぐろ塾の安田2023東大の文系数学の第１問で使ったばかりです(笑)
そこでの使用法通りに、２数の場合の両辺を２倍した形で暗記してる人も多いのでは？でも…
上の形で暗記すべきです、両不等式の左辺が平均になっていることが分かるから。この君たちが小学生時代から当たり前に使っている「平均」＝「足し算の平均」＝「相加平均」です。
めぐろ塾の安田だから「相加相乗平均」って言葉の通りに暗記すればいい。右辺は「掛け算の平均」＝「相乗平均」になってて、この「掛け算の平均」の取り方さえおさえちゃえば、「足し算平均≧掛け算平均」ってだけ！
では「掛け算の平均」の取り方ですが…
\(a\:,\:b\) の掛け算の平均は、取りあえず
\(ab\)
って掛けといて…
\(a\:,\:b\) の両方に注目すると \(ab\) は２次式だから、
掛け算平均は、\(\sqrt{ab}\)
同じように考えれば、\(a\:,\:b\:,\:c\) の掛け算の平均は、取りあえず掛けて \(abc\) 、これは３次式だから、掛け算平均は、\(\sqrt[3]{abc}\) って求められます。
めぐろ塾の安田ルートは１／２乗、３乗根は１／３乗って書いても大丈夫です。これで「相加相乗平均の不等式」を真面目に暗記する必要がなくなりました(笑)
等号成立条件は、
全部一緒なら、足し算平均も掛け算平均も一緒っぽい
ってノリでおさえてくれればオッケーです(笑)
因みに少し大学内容に入ってしまいますが、\(n\) 個になっても足し算平均と掛け算平均の取り方は変わらないので、
正の \(n\) 個の数 \(a_1\:,\:a_2\:,\:\cdots\:,\:a_n\) について、
\(\displaystyle\frac{a_1+a_2+\:\cdots\:+a_n}{n}\:\)≧\(\:\sqrt[n]{a_1\cdot a_2\cdot\:\cdots\:\cdot a_n}\)
が成立し、等号成立は、\(a_1=a_2=\:\cdots\:=a_n\) のときである
も、上の内容から作れてしまいます。
等差・等比中項
めぐろ塾の安田あんま使わないんだけどね～(笑)
等差・等比中項
３数 \(a\:,\:b\:,\:c\) がこの順で、
（Ⅰ）等差数列のとき、\(2b=a+c\) が成立
（Ⅱ）等比数列のとき、\(b^2=ac\) が成立
等差数列のとき、公差を \(d\) とすると、\(d=b-a=c-b\) 。等比数列のとき、公比を \(r\) とすると、\(r=\displaystyle\frac{b}{a}=\displaystyle\frac{c}{b}\) 。
めぐろ塾の安田ってゆー風に公差や公比を消去すればすぐに導けるんだけど、この形を意識してないと文字数多くなって混乱するってゆー悪質な内容(笑)
この式も「足し算の平均」と「掛け算の平均」を意識すれば、暗記価値がなくなります！
（Ⅰ）等差数列のとき、真ん中の \(b\) は \(a\:,\:c\) の「足し算の平均」っぽいから、\(b=\displaystyle\frac{a+c}{2}\)
（Ⅱ）等比数列のとき、真ん中の \(b\) は \(a\:,\:c\) の「掛け算の平均」っぽいから、\(b=\sqrt{ac}\)
めぐろ塾の安田に決まってるじゃん(笑)因みに等比数列の場合、\(b\) が負の場合に備えて両辺を２乗しなきゃいけないんだけど、ルートきたら皆２乗するでしょ？
だから多分大丈夫。記述式だとルートで立式した部分書くと減点対象だけど、まーこれくらいは減点されてもいいよ(笑)
まとめ
数学の公式は、絡めて覚えれば忘れない！
めぐろ塾の安田…んだけど…もう一度言うね…
我ながら「凄く限定的」(笑)
でもこの記事で、君の「数学の公式」に対する苦手意識が少しでも解消されたら嬉しいな！
君の大学受験が最高の結果になることを祈ってます！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
