数学が苦手な高校生必見！数学が得意になる方法を伝授！！
いきなりですが、１つ質問です。
めぐろ塾の安田君は、「数学」をどんな科目だと思っていますか？
「思考力が問われる科目」？
「天才さん専用科目」？
この質問に君がどう答えるかで、君が今「数学」が得意か苦手かが分かります。
結論：数学はただの暗記科目！
めぐろ塾の安田この結論に納得いく人はもうこの記事読まなくていいですよ(笑)
多分ある程度「数学」が得意な人だと思うんで。
数学はただの暗記科目です！
少なくとも、どの大学でも暗記で合格点には辿り着けます！！
めぐろ塾の安田ただ…指導者側も失念してる人が多いんだけど…くれぐれも間違えて欲しくないのは…
問題の形から暗記すること！
極端にカンタンな例を挙げると…
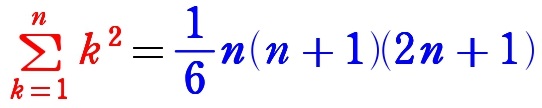
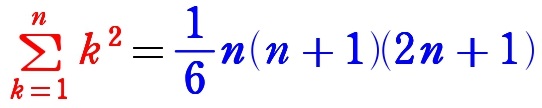
公式の右だけ覚えて安心しないで、
左もしっかり覚えろ！
ってこと。授業してても多いんですよね…この公式書いて…
めぐろ塾の安田覚えろ！
覚えました！
めぐろ塾の安田よし言ってみろ！
左って…どんな形でしたっけ？
結果を覚えていても、いつ使うのかを暗記していなければ使えるわけはありません！
解法ばっかり暗記しようって人が多いんだけど、常に、
この問題を見たら… → この解法
というようにケースの暗記を怠らないこと！
めぐろ塾の安田指導者側もケース暗記の大切さを失念しちゃってる人は多いです。
かく言う僕もたまに問題の解説時に失念しちゃって、「ゴメンゴメン」って説明し直すことありますね(笑)
具体例～基礎編～
ちょうどいい感じの問題が2023神戸大↓で出題されていたので…
理系数学の２．(1)を取り上げます。
問題
暗記すべきこと
めぐろ塾の安田「２次方程式の解配置問題」と呼ばれる超有名問題ですが、このタイプの問題で暗記すべきは…
２次方程式の解の範囲が登場したら…
↓
「軸・判別式・端点値」を調べてりゃオッケー
ってとこです。他にも、
- ２解が異なる区間にある場合は、端点値のみ調べればオッケー
- ２次の係数に文字定数（本問でいうと \(a\) と \(b\) ）が付いてる場合は、まずそれで割る
- 文字定数が１文字１次の場合は、定数分離法の方が楽なことがほとんど
とか細かい暗記もあるけど、一番大事な暗記は上の通り。少なくとも、上さえ覚えてれば近い解答にはなって部分点はもらえます。
解答
本質的な説明
一応次項で用いるので、なぜ２次方程式の解の範囲が登場する問題で「軸・判別式・端点値」を調べるのかを説明しておきます。それぞれの意味合いが分かっている人は、「具体例～応用編～」まで読み飛ばしてしまって構いません。
めぐろ塾の安田グラフは全て「形」と「位置」によって決定されます。例えば…
| 形 | 位置 | |
| 直線 | 傾き | 通る１点 |
| 円 | 半径 | 中心 |
２次関数のグラフ（放物線）の場合、位置を決定するのが「頂点」です。本問の場合、
\[\begin{split}y&=x^2+ax+b\\&=\left(x+\displaystyle\frac{a}{2}\right)^2-\displaystyle\frac{a^2}{4}+b\\&=\left(x+\displaystyle\frac{a}{2}\right)^2-\displaystyle\frac{a^2-4b}{4}\end{split}\]
より、頂点は \(\left(-\displaystyle\frac{a}{2}\:,\:-\displaystyle\frac{D}{4}\right)\) となり、「軸」が \(x\) 座標に、「判別式」が \(y\) 座標に登場していることが分かるでしょう。これで放物線の位置を「頂点」で正しく定めても…
こーなっちゃうとマズい
ので、「端点値」\(f(0)>0\) にし、形等の微調節を行うことで、
「\(f(x)=0\) の解」＝「\(y=f(x)\) と \(x\) 軸の共有点」が \(x>0\) に２つ存在
するようにしています。まとめると…
| 軸 | 放物線のヨコの位置を決める |
| 判別式 | 放物線のタテの位置を決める |
| 端点値 | 放物線の形等の微調整 |
めぐろ塾の安田このレベルの問題なら完全暗記でいいんだけど、次項で扱う解法を理解する上ではこの本質が重要になります。
具体例～応用編～
めぐろ塾の安田大学受験数学における、いわゆる「応用問題」と言われる問題は２タイプに分かれます。
１タイプ目は、
↑の問題１(4)や…
↑の第６問のような、高レベルなひらめきや思考力が問われる「天才さん専用問題」(笑)
めぐろ塾の安田こーゆーのは解けなくてオッケーです。合否にほとんど影響しないんで。凡人でも解けなきゃいけないのは２タイプ目の…
典型的暗記がたくさん複合された応用問題！
ちょうど「具体例～基礎編～」と対応した応用問題が2023阪大↓で出題されていたので…
文系数学の１を取り上げます。
問題
暗記すべきことと解答
三角関数の問題ではまず…
↓
角度と種類を統一して、置き換え
という典型暗記を発動します。ここで「２倍角の公式」を使いますが、覚えてない人はこの記事のここをご覧くださいm(_ _)m
ほんで…
ですね。変数が \(\theta\) から \(\sin\theta=t\) に変わるので、定義域も変換しておきます。取りあえずこれで↓まで解答が書けます。
これで「具体例～基礎編～」で暗記したケース、「２次方程式の解配置問題」になったので…
２次方程式の解の範囲が登場したら…
↓
「軸・判別式・端点値」を調べてりゃオッケー
めぐろ塾の安田じゃ解けないんですよね、この問題(笑)
↓のようにたくさん放物線 \(y=f(t)\) が描けちゃうから困っちゃう。
ここで「具体例～基礎編～の本質的な説明」が重要になります。今大事な \(t\) 軸と解の区間 \(-1≦t≦1\) はヨコなので、放物線のヨコの位置を決める「軸」が解の区間の右に外れているとしましょう。
放物線 \(y=f(t)\) が１通りになってハッピー
めぐろ塾の安田です。ま～一応説明入れましたけど、これも暗記しておいた方がいいですね↓
放物線がたくさん描けて困ったら…
↓
「軸」の位置で場合分け
後は各場合で「判別式・端点値」を調べますが、どっちかがいらなくなる場合も多いです。また、解答ではド・モルガンの法則で説明していますが、
「軸」が区間内の場合は…
↓
「端点値」は「または」で処理
ってことまで暗記してるとなお良し。これで↓まで解答が完成。
めぐろ塾の安田最後に図示ですが、結局この系統の問題で一番時間喰われちゃうのって図示部分なんですよね…なんでまた暗記↓(笑)
本問の「２次方程式の解配置問題」部分以降は、
「\(t\) が \(-1≦t≦1\) を動くときの直線 \(y=-tx+1-2t^2\) の通過領域を図示せよ」
というように「直線の通過領域」の問題として書き換えることもでき、図示結果は一致します。この場合、判別式条件から出てくる放物線は「包絡線」と呼ばれ、
端点値条件 \(f(-1)\:,\:f(1)\) から出てくる直線は「包絡線」と必ず接し、
「包絡線」上を滑らせた領域が正解
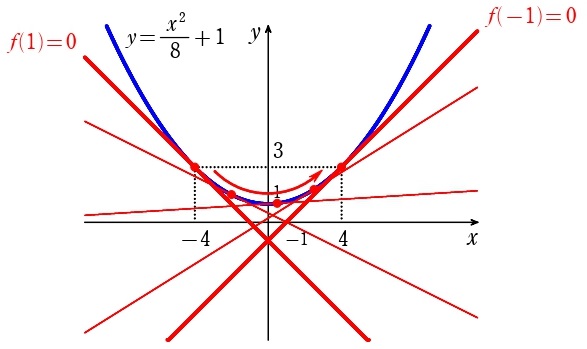
であることを暗記しましょう(笑)図示スピードが格段に上がり、ミスもなくなります。以上で終了↓
具体例～実践編～
おいおい…ここまで暗記するのかよ…
って思った人もいるかもしれませんが…
めぐろ塾の安田上位大学を受験するなら暗記しておくべき！阪大は2022理系数学の３でも同系統の問題を出題しています↓
問題
暗記すべきことと解答を途中まで
めぐろ塾の安田減点されそうなところとかを上手く回避した解答を、途中まで僕が作っといてあげます↓(笑)
これで「具体例～応用編～」でも話した「直線の通過領域」の問題となりました。これを「解配置問題」に持ち込むための暗記は、
文字定数を含むグラフの通過領域を求めるときは…
↓
文字定数の方程式と見て、「実数解を持つ」と言い換える
です（今回の文字定数は \(t\) ）。この問題ではあんま必要ないんだけど、「具体例～基礎編～」でちょろっと話した「２次の係数で割る」とかも僕がやっといてあげます↓(笑)
これで「具体例～応用編～」と全く同じケースになりました！同じように領域を求めて、第１象限だけに斜線を引けば大丈夫です！！
残りの解答は自分で作ってみよう！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
めぐろ塾の安田できたかな？
この後の図示も、
端点値条件 \(f(1)\:,\:f(2)\) から出てくる直線は判別式条件の「包絡線」と必ず接し、
「包絡線」上を滑らせた領域が正解
って暗記に成功した人はスピーディーに描けたんじゃないでしょうか？でも…
めぐろ塾の安田流石にここまで覚えなくていいだけど(笑)
端点値条件から出る直線と包絡線は、場合分けの変わり目で接する
ってことまで暗記できると、図示が１分くらいで終わります(笑)計算がほぼ２直線の交点の \(x\) 座標 \(\displaystyle\frac{1}{3}\) を求めるだけになるので。
まとめ
めぐろ塾の安田数学はただの暗記科目です！
極力詳しく説明してきましたが、応用編以降で題材にした問題は受験数学でも標準以上の難易度とされる内容なので、高２以上じゃないと理解は難しいかもしれません。
この記事の内容は理解できなくてもいいです。ただ…
数学できる人ってここまで暗記してるんだ…
ってゆー認識だけ持ってください。
オレって数学的センスないもんな～
なんてマインドでいると、そもそも暗記する気がなくなっちゃいます。これが一番ダメ！
めぐろ塾の安田大学受験数学の講師を20年やってるけど、僕は大して数学センスないよ(笑)暗記してるから解けるだけ。
少なくとも、どの大学でも暗記で合格点には辿り着けます！！
ただ…この記事内で徹底してきた通り…
この問題を見たら… → この解法
というようにケースの暗記を怠らないこと！
これを意識するだけで、今後の君の数学の勉強がかなり良い方向に傾くはずです！！
めぐろ塾の安田めぐろ塾では、頻出なケースとその解法の暗記が終わるまで家に帰さなかったりします↓(笑)
こんな過酷な環境下に身を置きたい方はお問い合わせください↓(笑)
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
