2023千葉大【理系数学】解説・解答・講評

2023千葉大学の理系数学の解説・解答・講評をお届けします!
千葉大の数学の特殊性

↑でもお話ししているんですが…
千葉大の数学の入試では、
文系数学と理系数学が同じ冊子で配られる!
 めぐろ塾の安田
めぐろ塾の安田ことは、千葉大を受ける人は覚えておいてください。
かつ…
理系数学では、学部・学科によって解く大問が変わる!
ことになるので、理系の人は解く大問を間違えないように気を付けましょう!
2023では以下の通りです。
| 学部・学科等 | 解答する問題番号 | 試験時間 |
|---|---|---|
| 教育学部(中学校コース数学科教育分野) | 3~8の6問 | 150分 |
| 理学部(物理学科、化学科、生物学科、地球科学科) 工学部 園芸学部(園芸学科、応用生命科学科、緑地環境学科) 薬学部 先進科学プログラム(物理学関連分野、工学関連分野) | 4~8の5問 | 120分 |
| 理学部(数学・情報数理学科) | 4~9の6問 | 180分 |
| 医学部 | 5~9の5問 | 120分 |
本記事では理系数学を対象とするので、大問4~9の解説・解答・講評となります。
教育学部(中学校コース数学科教育分野)を受験する人は、大問3については文系数学の記事をご覧ください。
4
問題


考え方
(1)は、微分して増減表を作って最大値を読み取るだけ。文字定数が2つあるけど、千葉大受けるようなら混乱しちゃダメ!
(2)・(3)では以下の極限公式を使いますが…
指数・対数関数の極限公式
\(\displaystyle\lim_{x\to0}\displaystyle\frac{\log(1+x)}{x}=1\) 、 \(\displaystyle\lim_{x\to0}\displaystyle\frac{e^x-1}{x}=1\)



多くの教科書や参考書は公式として明示してないんですよね…これ。
そんなに使用頻度は高くありませんが…
覚えてなかった人はこれを機に覚えておきましょう!↓のようなグラフのイメージを持っておくと覚えやすくなります。


解答


5
問題


考え方
(1)は、\(\overrightarrow{\textrm{OA}}\) と \(\overrightarrow{\textrm{OB}}\) が1次独立であることの証明です。



大学受験数学の講師歴20年ですけど、初めて見ました(笑)
まーでも初見でも迷うことはない問題でしょう。解答では背理法で、\(\overrightarrow{\textrm{OB}}=k\overrightarrow{\textrm{OA}}\) として序文の条件から矛盾を導いて証明しています。
(2)は、正射影ベクトル↓を暗記していれば一瞬で片付きます。
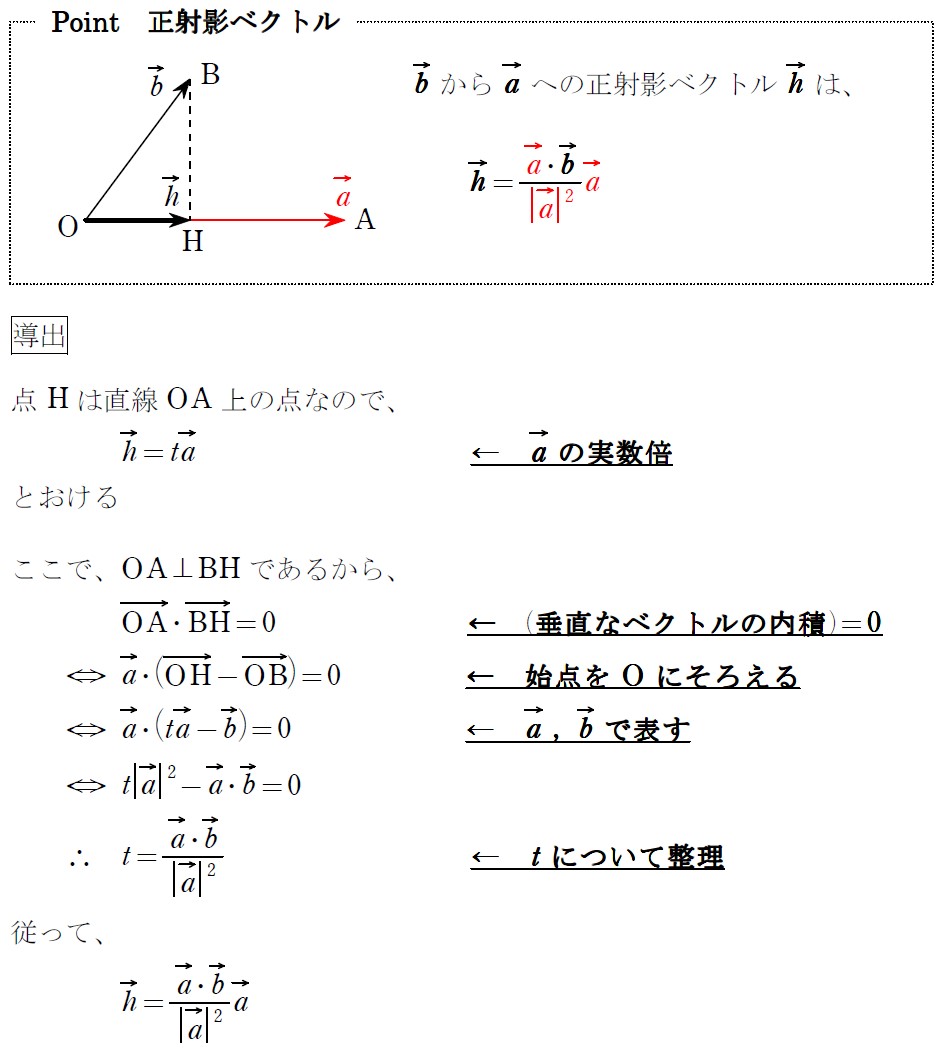




僕は、「垂線の足へのベクトルを求めるときは、乗ってる方を書きまくる」って暗記してます。
ま~でも導出のように、未知数(導出では \(t\))をおいてやっても大して時間はかかりません。正確に当ててください。
(3)は、(2)を誘導として捉え、
\(\overrightarrow{\textrm{OR}}=\overrightarrow{\textrm{OP}}+p\overrightarrow{\textrm{HB}}\) と表せる
↓
(2)からの処理と全く同様にして、未知数 \(q\) で \(\overrightarrow{\textrm{OR}}\) を表す
↓
(1)より \(\overrightarrow{\textrm{OA}}\) と \(\overrightarrow{\textrm{OB}}\) は1次独立なので、係数比較
という、以前の記事でも紹介している「1次結合の<解法2>」で処理します。



(4)は正直オマケ(笑)
「外接円の中心」=「外心」は「垂直二等分線の交点」なので、(3)の \(t\) に \(\displaystyle\frac{1}{2}\) を当てはめて終了です。
外心なんてもっとカンタンな1次結合の方法あるじゃん…
って思う人もいるかもしれないけど、しっかりと誘導に乗って、出題者の意図に沿った解答を作りましょう(笑)
解答




6
問題


考え方
(1)は2回なので、具体的にどの目がどの順で出るか考えるだけ。
(2)・(3)は「n回試行の確率」の<方針1>「n回の過程を具体的に考える」、<方針2>「確率漸化式」のうち、<方針2>「確率漸化式」ってのはすぐ分かると思うんですが…



「ルール」が複雑すぎる…(笑)
結局…
\(n≧1\) で \(a_n=1\:,\:3\:,\:4\:,\:5\:,\:6\:,\:7\) であることを把握
↓
各場合で1~6の目が出たら \(a_{n+1}\) がどうなるかの30通り以上を全て書き出す
しかありません。
これで(2)は、\(a_n=7\) のとき以外、\(a_{n+1}=7\) となる確率が \(\displaystyle\frac{1}{6}\) であることが分かるので、\(a_n=7\) のときの確率を \(p_n\) とすれば、
\[p_{n+1}=p_n+\displaystyle\frac{1}{6}(1-p_n)\]
が立式できて片付きます。



試験時間的にも(3)は解けなくて大丈夫な気がする(笑)
他社さんは表から上手い解法を見つけていましたが、凡人の僕にはムリでしたm(_ _)m
なので、確率漸化式で困った場合は、面倒でも全ての確率を設定して連立漸化式を立てれば何とかなる、とゆー経験則に従い、5数列を設定して連立漸化式を5つ立てた後、式的に対処を考える解答を作成させて頂いております(笑)



こーゆー場合、解答のように右辺をずらして書いて、係数の和が一致していることを確認する、なんてゆーのもテクニックの1つです。
因みに授業してると漸化式の有効範囲を苦手にしている生徒って多いんですが…解答を例に説明すると、
\(n≧1\) で、\(q_{n+1}+u_{n+1}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{5}{6}\right)^{n-1}\)
↓ \(n\) を●と思う
\(●≧1\) で、\(q_{●+1}+u_{●+1}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{5}{6}\right)^{●-1}\)
↓ ●に \(n-1\) を代入
\(n-1≧1\) 、つまり \(n≧2\) で、\(q_{n}+u_{n}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{5}{6}\right)^{n-2}\)
というように、\(n\) を●って思って、冷静に範囲にも代入するだけです。難しく考えないように!
解答


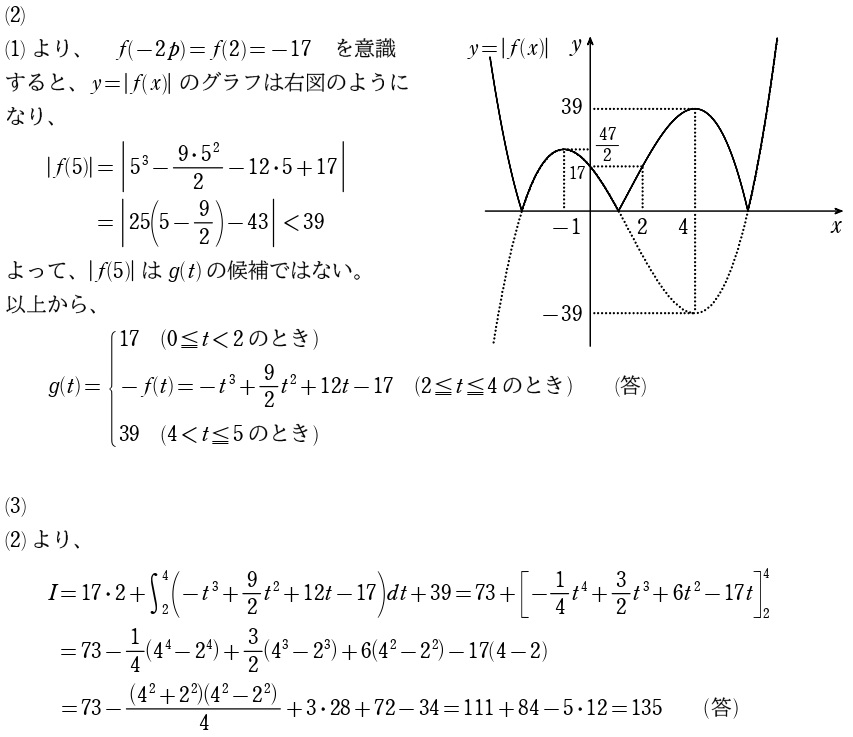

7
問題


考え方
(1)は、合成して \(-1≦\sin●≦1\) を使うだけ。他社さんは皆 \(\cos\) に合成していましたが、同じ解答書いてもしょうがないんで…



あえて皆が慣れてるはずの \(\sin\) 合成でやってみました(笑)
勝負は(2)から。「絶対値関数の定積分」なので、「グラフの上下」や「面積」を考えることで絶対値を外します。ここで(1)の合成角が有名角ではなく \(\alpha\) とおいたので、
解答の赤字部分のように、\(f(x)\) の周期性から、置換積分で \(\alpha\) のズレをなくす
という処理が必要になります。めぐろ塾↓では授業で扱うので的中!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
因みにこのときの核となる、
\[\displaystyle\int_{-\alpha}^{0}f(t+\alpha)dt=\displaystyle\int_{2\pi-\alpha}^{2\pi}f(t+\alpha)dt\]
は \(t+2\pi\) を置換することで厳密に証明できますが、被積分関数 \(f(x)\) の \(2\pi\) 周期性から当たり前、かつ解答が長くなり過ぎるので省いています。実際、この部分の証明は省く参考書も多いので。
解答の青字部分では、場合分けを3つから2つに減らすために、やはり \(g(t)\) の \(2\pi\) 周期性から積分区間を変更しています。これはやらなくてもいいかもしれません。場合分け3つでも正確に当ててください。



絶対値関数の定積分では、最初の場合分けの変わり目部分の代入を2倍しておけば、後の同値の代入は必要なくなる、ってテクニックを知っていれば、場合分け3つでも大した計算じゃない!
(3)は、フツーなら \(0≦t≦\pi\:,\:\pi<t≦\displaystyle\frac{4\pi}{3}\:,\:\displaystyle\frac{4\pi}{3}<t<2\pi\) で場合分けするところですが、
ここまでで十分ボリュームあるから、もう場合分けなんかしたくない
って思いましょう(笑)領域の広い0~ \(\displaystyle\frac{4\pi}{3}\) のとこに最大値があるに決まっています。解答では厳密に面積で論証していますが、論証が甘くても減点覚悟で答を当てにいった方がいいでしょう。
解答




8
問題


考え方
「複素数平面」からの出題、極形式とド・モアブルの定理を用いた「\(i\) のn乗根」という有名内容です。
(1)は、(2)以降と同様の処理でも解けますが、\(-i=i^3\) と考えて因数分解公式
\[a^3+b^3=(a+b)(a^2-ab+b^2)\]
で解いてしまうのが一番カンタン。
(2)は「\(i\) の100乗根」なので、\(z=r(\cos\theta+i\sin\theta)\)(\(r>0\))とおいて100個の解を整数 \(k\) で表し、指定範囲に収まる \(k\) の個数をカウントする。
(3)も同様の流れですが…



(3)の最後は完全に整数問題になります…
/12 はメンドくさすぎるので、分子が奇数であることに注目、偶数に是正して2で約分
↓
/6 ならしらみつぶせるから、6で割った余りで場合分けして範囲の端を整数に是正
って感じで…
整数問題に長けた人であれば、
ど~せ答は「nを6で割った余りがいくつ」って形で解答するんでしょ~
ってとこまで読める問題ではありますが…
どー解いても計12ヶ所の整数への是正が必要なので面倒です。(2)までの完答は必須として、(3)は「6で割った余りに注目」する部分くらいまで書ければ及第点に思えます。
解答






9
問題


考え方
(1)は、\(h(x)=tx-f(x)\) が \(x\) の4次関数になるので、微分して増減表を作るだけ。
(2)からは \(f(x)\) が具体的に与えられない「抽象関数」の問題です。苦手にしている人も多いと思いますが…



最大・最小問題の場合、面倒な微分計算がないのでカンタンなことが多い!
ことを覚えておきましょう。本問も、
\(h'(x)=0\) の解が、\(y=t\) と \(y=f'(x)\) の交点と考えることでただ1つと分かる
(定数分離法)
↓
これを \(x=\alpha\) とおくと、\(h(x)\) の増減表が作れて(2)が終了
↓
\(t=f'(\alpha)\) より、\(st-g(t)\) が \(\alpha\) の関数として表せる
という有名処理を面倒な微分計算なしで実行できるので、具体的な関数の問題よりもむしろカンタンです。



ただこの問題が意地悪なのはこの後…
最初僕が書いてしまったこの解答↓のどこが間違っているか分かりますか?


間違ってるとこ
\(f'(x)\) は微分可能と言われていないので、\(f^{\prime\prime}\) を使ってはいけない!
\(q'(\alpha)\) 以降の解答は間違いです。まあこの解答でも部分点はもらえると思いますが(笑)
模範解答としては、\(f^{\prime\prime}\) の使用を回避するため、\(f(x)\) に平均値の定理を利用して \(q(\alpha)\) を \(f’\) のみの式に書き換える必要があります。
このクソ解答を打ち終わって、他社さんの解答を見て間違いに気づきました…
大学受験数学のプロ講師歴20年なのに、引っかけにはまってしまいました…



生きててすいませんm(_ _)m
解答




講評
千葉大の理系数学は、やはり例年難しいです。ただ2022と比較しても…
| 解答方式 | 試験時間・大問数 | 難易度 |
|---|---|---|
| 記述式 | 学部・学科によって変わる | やや難化 |
じゃないでしょうか?



「手が付けられないほど難しい」って問題がないのは例年通りなんですが…
- 6・8は共に状況をしらみつぶす必要がある
- 7は論証方法に迷う
- 全体的に文字定数が多すぎる
って感じで、例年よりも「難しい」ってより「面倒くさい」ので。
理系学部・学科全てで共通問題である5(ベクトル)と8(複素数平面)(1)・(2)は簡単なので、これの完答はマストです。
4も指定されている学部・学科の人は完答して欲しいところ。
6は(1)までしか解けなくても大丈夫そう、解けた人は少ないと思います。
7は論証不備で減点されても、答を当てるの重視でいった方がいい。数学得意な人でこれのキレイな論証考えすぎて時間喰われちゃった人は結構多そうな気がします。それなら他の問題解いた方がコスパはいい。
8(3)は「6で割った余りに注目」する部分まで書ければ及第点。
9は僕のクソ解答くらい書ければ及第点(笑)



こんな感じじゃないでしょうか?
記事が結構長くなっちゃったので、ミスとか見つけたらご連絡頂けると助かります↓(笑)もちろん「めぐろ塾」へのお問い合わせも大歓迎


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








