2023上智文系【数学TEAP利用】解説・解答・講評

2023上智大学文系学部のTEAPスコア利用方式の数学の解説・解答・講評をお届けします!
経済学部の共通テスト併用方式の数学については↓の記事をご覧ください。

1
問題

考え方
\(\sin x\) と \(\cos x\) の対称式の最大・最小という、超典型問題です。問題文の誘導にもある通り、基本対称式の一方 \(\sin x+\cos x=t\) とおき、この両辺を2乗して必ず成立する対称式 \(\sin^2x+\cos^2x=1\) を使うことで、もう一方の基本対称式 \(\sin x\cos x=\displaystyle\frac{t^2-1}{2}\) を導きます。合成によって、\(-\sqrt{2}≦t≦\sqrt{2}\) という変域をチェックするのを忘れないように。
 めぐろ塾の安田
めぐろ塾の安田あまりにも良く出るんで…めぐろ塾だと暗記させて僕の前で復唱する↓のを義務づけています(笑)コイツはそこの前でつまづいちゃいましたが…
合格するためには絶対外せない問題でしょう。多少時間を使ってでも、確実に当ててください。
解答


2
問題


考え方
全て問われているのは長さですが、ベクトルの絶対値形式で問われていることからも分かる通り、一次結合ができれば解決します。解答のように、最初に基準となるベクトルを \(\overrightarrow{\textrm{AB}}=\overrightarrow{b}\:,\:\overrightarrow{\textrm{AC}}=\overrightarrow{c}\:,\:\overrightarrow{\textrm{AD}}=\overrightarrow{d}\) と設定し、\(\overrightarrow{\textrm{AE}}\) をこれらで表しておくのが良いでしょう。
(1)は、これらで一次結合しなくても、図形的に解決できます。
(2)は、序文の垂直条件から、「一次結合<解法3>」。
(3)は、(2)の結果を利用し、2乗して内積計算。
(4)は、「一次結合<解法2>」。
典型ではありますが、
- 空間なので、計算量は少なくない
- (2)で計算ミスすると、(3)以降は連動して全滅になっちゃう
問題です。(2)を正確に計算できたかが、合否を大きく分けたでしょう。
解答




3
問題


考え方
問題文を見てビビる人もいるかもしれませんが、問題自体は全く難しくありません。
(1)は、選んだ1人がA型感染、B型感染、感染してないで場合分けして計算。
(2)は、条件付き確率。(1)の場合分けの結果を活用。
(3)は、(1)・(2)と同じことを、検査2回で実行するだけ。



ただ…この問題…個人的には最悪の出題に思えてしまいました…
20年以上前から↓のように…
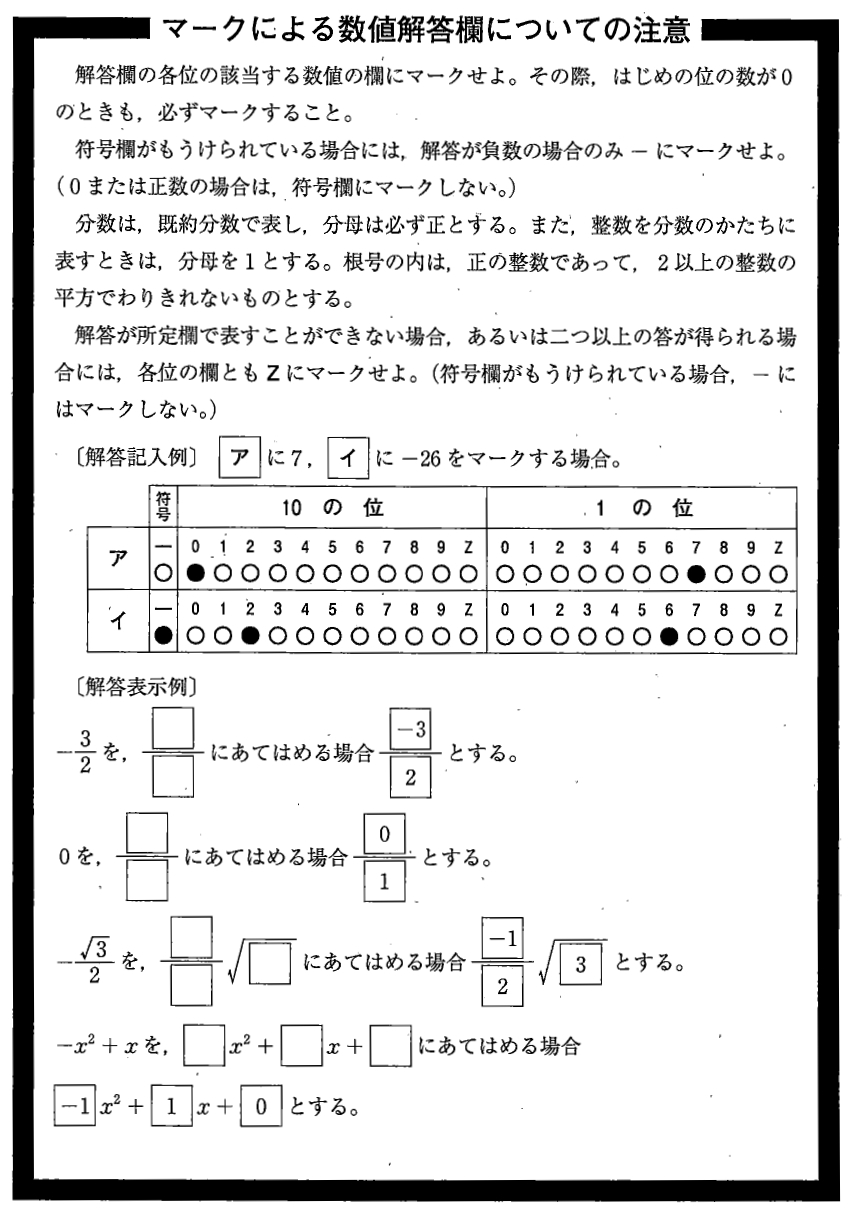

カタカナ空欄は、\(-99\) ~ \(99\) の整数値をマーク、当てはまらない場合はzをマークする
が基本で、
zをマークすることは(ほぼ)ない!
なんですが…この問題は「ノ」と「ヒ」の空欄が3ケタになります。



上智の数学は文理で合計20セットくらい解いてますが…
恥ずかしながら僕は3ケタ解答に出会ったのが初でした…
気になって調べたら2017でもありました…
上智大学の公式解答を見る限り、どうやら「ノ」と「ヒ」のマークシートには百の位も用意されていたようです。
「カタカナ空欄は \(-99\) ~ \(99\)」って思いこんでた僕は、「絶対計算ミスったろ?」って思って10回くらい計算確認しちゃいましたね…過去問対策してる人で試験中に僕と同じ感じで時間使っちゃった人がいませんように…ちゃんとマークシート見て3ケタ解答って気づきましたように…
※因みに上でzマークを「ほぼ」ない、としたのは、上智大学の公式解答が本問の(3)の解答全てをzマークでも良いとしていたからです。「作問不備とかあったのか?」と思って考えてみましたが、見つかりませんでした。この謎を解けた人がいたら教えてください、ラーメン奢ります(笑)
今まで生徒に…



上智の数学のカタカナ空欄は \(-99\) ~ \(99\) の整数値マークだよ~
って指導しちゃってたんですが…この苦い経験を活かし…
上智の数学のカタカナ空欄、たまに3ケタ解答あるよ!
って今後めぐろ塾↓では教えたいと思います…人間日々勉強ですね、精進しますm(_ _)m


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答




4
問題


考え方



小問集合です。
(1)・(2)は、近年の上智数学で頻出の「命題・集合」形式をとっていますが、冷静に条件を噛み砕けば、問われている内容は標準的です。
(1)は、条件 \(p\) を正方形って認識できれば、円との包含関係ってだけ。
(2)は、2変数1次不定方程式で \(A\cap B\) を考え、\(A\cup B\) は周期数列に持ち込みます。因みに後者も3と同じく3ケタ解答です。非常に稀な3ケタ解答を1セットで2回もやってくるとは…(笑)



(3)は時間内解答は厳しいと思います。
通過領域は図形的にすぐ読み取れるんですが、交点の値が汚くなって、変な直線まで絡んでくるので。
等積移動し、三角形と放物線領域に分ける
↓
三角形の面積は次数下げ、放物線領域の面積は主に解と係数の関係を利用
というように、考え得る限りベストな計算を実行しましたが、これでも計算量は多いです。下手に計算に取り組むより、他の問題に時間を充てた方が良いでしょう。
解説






講評



2022と比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式 | 90分 | 4問 | やや難化 |
に思えます。計算ボリュームがかなり増えました。
- 2の(2)で計算をミスらず、2全体を完答できたか
- 3の問題文の見た目にビビらず、カンタンな問題って気づけたか
が勝負を分けたと思います。



1と2を完答して、3と4のいくつかを当てれば及第点でしょう。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!







