2023東北大【理系数学】解説・解答・講評
2023東北大学の理系数学の解説・解答・講評をお届けします！
文系数学については↓の記事をご覧くださいm(_ _)m
１
問題
考え方
取り出したものを戻さずに取り出していく、「非復元抽出」の問題です。
(1)は、Ａが白玉を、Ｂが赤玉を取り出し続けるだけ。
(2)は、Ａが奇数回目で初めて赤玉を取り出す確率（Ｂはそれまでひたすら赤玉です）を足し合わせるだけ。最大でも７回なので、シグマを使う必要もありません。
「非復元抽出」で順番が問われている場合
↓
順列（パーミテーション）で一気に取り出す
という原則に従って解答を書きましたが…
めぐろ塾の安田最大でも９回なので、各回の確率を計算しちゃっても大丈夫な小学生問題です(笑)計算ミスにだけ気を付けて！
解答
２
問題
考え方
(1)は３倍角の公式でも解けますが、和積公式で解くのが普通でしょう。「最小のもの」という表現からも分かる通りですが、定義域が正としか言われていないので、整数 \(n\) を使って解を求めてください。
(2)は、(1)の結果を利用すれば、\(p(m)\) をガウス記号で表すことができます。
ガウス記号
\([x]\) ： \(x\) を超えない最大の整数
めぐろ塾の安田ガウス記号って苦手意識を持ってる人が多いと思うんだけどね(笑)
基本的には…
\(x-1＜[x]≦x\)
ガウスを幅１ではさむ
\([x]≦x＜[x+1]\)
幅１のガウスではさむ
のどちらかで対処します。
本問は前者からのはさみうちの原理。教科書にも載ってる内容で、計算量も少ないので、確実に完答しましょう！
解答
３
問題
考え方
(1)は、係数が \(n\) の式になっているタイプの漸化式を解く問題です。
係数がプラス方向にズレすぎている
↓
すき間をかけることで１項ズレに
します。本問の場合は \(n\) と \(n+2\) のすき間に存在する \(n+1\) をかけることで、階差数列が分かるタイプの漸化式に持ち込めます。
めぐろ塾の安田東北大だから \(n=1\) のときと \(n≧2\) のときで違う式になることを期待したんですが、こーゆーひっかけもなくて拍子抜け(笑)
因みに、
係数がマイナス方向にズレている
↓
全体で割ることで１項ズレに
するんですが、こーゆーのも知りたい人はめぐろ塾↓にどうぞ(笑)
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
(2)も、
∑(分数関数) → 部分分数分解して、「並べて書くと途中が消える」で計算
とゆー典型内容で等式を導くだけです。全体的な計算量も少ないので完答はマストに思えます。
解答
４
問題
考え方
この記事↓
の「１の５乗根の利用」関連の出題です。(2)の「ただし、\(r^5=1\) を満たす実数 \(r\) が \(r=1\) のみであることは、認めて使用してよい」という文章は、厳密性を補完するというよりは、
\(x^4+x^3+x^2+x+1=0\) に \(x-1\) かければ \(x^5=1\) が作れるからね～
という出題者側からのヒントでしょう。
全体的に、
めぐろ塾の安田オレ、このタイプの問題は完璧なんだぜ～
ってのをアピールするような解答を作成しましたが…ちょっと分かりにくいし、作成に時間もかかっちゃったんでタイパも悪いかも(笑)
(1)はフツーに整式の割り算で、(2)の(答)以降の記述はせず、(3)は２倍角の公式等で強引に計算しちゃっても良いでしょう。
解答
５
問題
考え方
(1)は、内積の定義式
\[\overrightarrow{\textrm{OA}}\cdot\overrightarrow{\textrm{OB}}=\left|\overrightarrow{\textrm{OA}}\right|\left|\overrightarrow{\textrm{OB}}\right|\cos\angle\textrm{AOB}\]
で \(\overrightarrow{a}\cdot\overrightarrow{b}\) を計算、「ＯＣとＡＢが垂直」から \(\overrightarrow{c}\cdot\overrightarrow{a}\) を計算するだけ。
(2)は、「１次結合＜解法３＞」の典型内容。
平面のベクトル方程式で、\(\overrightarrow{\textrm{OH}}=\alpha\overrightarrow{\textrm{OA}}+\beta\overrightarrow{\textrm{OB}}\) と表す
↓
ＣＨ⊥平面ＯＡＢ ⇔ ＣＨ⊥ＯＡ かつ ＣＨ⊥ＯＢ で \(\alpha\:,\:\beta\) を決定
（平面との垂直は、平面を作る２ベクトルとの垂直で処理）
(3)もほぼ同じ流れです。
平面のベクトル方程式で、\(\overrightarrow{\textrm{OK}}=(1-s-t)\overrightarrow{\textrm{OA}}+s\overrightarrow{\textrm{OB}}+t\overrightarrow{\textrm{OC}}\) （係数和が１）と表す
↓
ＯＫ⊥平面ＡＢＣ ⇔ ＯＫ⊥ＡＢ かつ ＯＫ⊥ＡＣ で \(s\:,\:t\) を決定
↓
\(\overrightarrow{\textrm{HK}}\) が \(\overrightarrow{c}\) の実数倍を示す
空間なので計算は楽ではありませんが、難易度・試験時間的に言って完答はマストでしょう。
解答
６
問題
考え方
最初の時点で(2)を見たので、この記事↓
で扱ってる、
めぐろ塾の安田「直線の通過領域」きたぁああああああああああああああー！！
って思って解配置問題にする気満々だったんですけどね…
めぐろ塾の安田端点Ｐの軌跡複雑すぎじゃね？
って思って作図してみると…
めぐろ塾の安田\(\overrightarrow{\textrm{PQ}}\) って常に \(\begin{pmatrix}1\\ 1\end{pmatrix}\) だから図形的に読み取れちゃうじゃん…
ってゆー、数学できる人の神経を逆なでする問題(笑)
- (1)でなぜか接線を求めさせている
- (2)で面積まで要求されてるから、面倒な解配置問題にはしないだろ
ってところから気づかないといけません。因みに端点Ｐの軌跡（\(y=f(x)\)）は凹凸まで調べて作図した方が良いでしょう。変曲点が存在すると、２曲線を線分で結べるとは限らなくなるので。
めぐろ塾の安田僕もここまでは気づけなかったんで、採点対象になってるかは微妙ですが…他社さんの解答を見て気づかせて頂きました(笑)
そしてこの問題が地獄なのは(2)後半の面積計算…これは時間内では当てられなくていいと思います(笑)
解答では、ベン図でのダブりの処理のように、
等積移動で平行四辺形と思える２面積の和 ー 重なった部分
で計算しました。各平行四辺形の面積は、
三角形の面積公式（座標平面）
\((0\:,\:0)\:,\:(a\:,\:b)\:,\:(c\:,\:d)\) を頂点とする三角形の面積 \(S\) は、
\(S=\displaystyle\frac{1}{2}|ad-bc|\)
の \(\displaystyle\frac{1}{2}\) をなくした形で計算しています。
解き終わった後、他社さんの解答を４つほど見て答え合わせ等をしたんですが、どの解答も細部まで見ると全然違ってて面白かったです(笑)
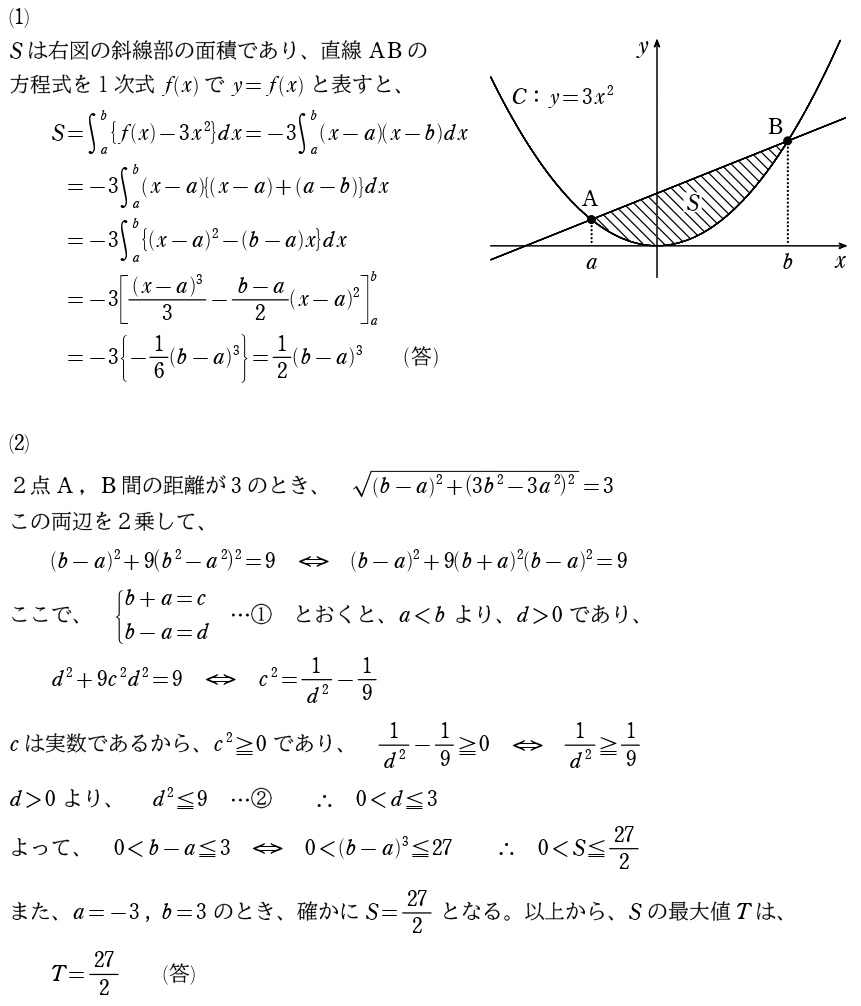
解答
講評
めぐろ塾の安田2022と比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 150分 | ６問 | やや易化 |
ですね。
大問６はキツすぎます、ってかこの記事作成の７割以上の時間をこの問題に使ってしまったので(笑)
でも大問１～５がかなりカンタン、計算もキツくないし。
「大問１～５までを完答、大問６を(2)の通過領域作図まで当てる」がベストストーリーだと思いますが、正直大問１～５までをどれなくミスなくとれたかの勝負だったでしょう。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
