2023阪大【文系数学】解説・解答・講評

2023年7月11日2023年10月28日

2023大阪大学の文系数学の解説・解答・講評をお届けします！

理系数学については↓の記事をご覧くださいm(_ _)m

１

問題

考え方

２倍角の公式を使って \(\sin\theta=t\) とおくことで、２次方程式の問題にできます。

めぐろ塾の安田

このとき、\(-1≦t≦1\) というように変域をチェックするのを忘れないようにしましょう！

結局 \(-1≦t≦1\) に \(f(t)=2t^2+at+b-1=0\) が実数解を持つ \(a\:,\:b\) の条件の図示という「２次方程式の解配置問題」となり、\(y=f(t)\) と \(t\) 軸が \(-1≦t≦1\) に共有点を持つときを考えるわけですが、\(y=f(t)\) のグラフの状態がたくさん考えられてしまうので、

\(y=f(t)\) の軸 \(t=-\displaystyle\frac{a}{4}\) が解の区間 \(-1≦t≦1\) に含まれるかで場合分け

するのが一番簡単で…

めぐろ塾の安田

めぐろ塾↓では授業で時間かけて２回扱うので的中！！

日本全国どこからでも受講可能！
完全個別指導コースあり（オンラインも可）！
初回面談・初回授業は完全個別で無料（オンラインも可）！

めぐろ塾の安田

初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓

お問い合わせ

03-6841-7626

電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。

頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。

X（Twitter）のDMからのお問い合わせ

ま～「的中」って喜べないような有名内容ではありますが(笑)軸が区間内に含まれる場合の端点値条件「\(f(-1)≧0\) または \(f(1)≧0\)」の導出はド・モルガンの法則でやっときました、この説明が生徒の反応が一番いいんで(笑)

因みに本問の「２次方程式の解配置問題」部分以降は、

「\(t\) が \(-1≦t≦1\) を動くときの直線 \(y=-tx+1-2t^2\) の通過領域を図示せよ」

というように「直線の通過領域」の問題として書き換えることもでき、図示結果は一致します。

めぐろ塾の安田

こっちの方が良く出題されますね。この場合、判別式条件から出てくる放物線は「包絡線」と呼ばれます。

結局この系統の問題で面倒かつミスが発生しやすいのは図示部分なんですが、

端点値条件 \(f(-1)\:,\:f(1)\) から出てくる直線は「包絡線」と必ず接し、
「包絡線」上を滑らせた領域が正解

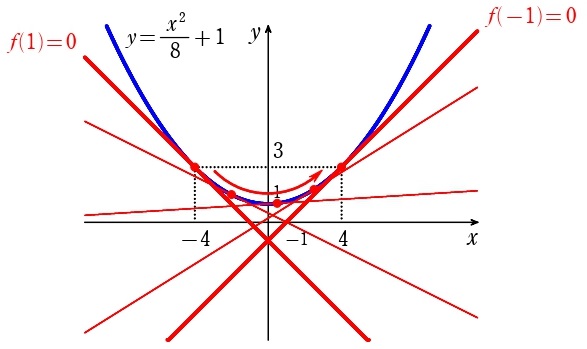
であることを知っておくと、図示スピードが格段に上がり、ミスもなくなります。

解答

２

問題

考え方

(1)は底の変換公式 \(\log_ab=\displaystyle\frac{\log_cb}{\log_ca}\) を使って \(a\:,\:t\) で表すだけ。

(2)は(1)で \(t\) の３次関数が立式できているので、やはり問題１と同様に \(-1≦t≦3\) というように変域をチェックすれば、「文字定数 \(a\) 入りの高次関数の最大値」という有名内容になるわけですが…

めぐろ塾の安田

うわ、簡単じゃん！って思ったら、この後はそこそこムズかった(笑)

こーゆー系統の問題って、

グラフを固定して、区間 \(-1≦t≦3\) を左右に動かす

って考えれば何とかなることがほとんどなんですが、この問題は最大値の候補点の上下の動きも複雑なんで、

\(f(2a)\) が候補に含まれるかを左右で場合分けしたら…
↓
各場合分けで、候補点の大小を差の正負で判断
（候補点比較法）

する必要があります。

めぐろ塾の安田

\(f(2a)-f(-1)\) に２乗のカタマリができて差の正負が判断しやすいってナイス作問なんですけどね、受験者の出来はあまり良くなさそう(笑)

解答

３

問題

考え方

めぐろ塾の安田

理系数学との共通問題。キレイな解答を作りたいのであれば、どの２つのベクトルを基準で考えるかが大切な問題です。

対称性からして、僕の解答のように \(2\overrightarrow{\textrm{OA}}+\overrightarrow{\textrm{OB}}=\overrightarrow{\textrm{OC}}\) と \(\overrightarrow{\textrm{OA}}+2\overrightarrow{\textrm{OB}}=\overrightarrow{\textrm{OD}}\) を基準とするのがベストでしょう。

これで、もう１つ登場している \(\overrightarrow{\textrm{OA}}+\overrightarrow{\textrm{OB}}\) も、

\[\overrightarrow{\textrm{OA}}+\overrightarrow{\textrm{OB}}=\displaystyle\frac{\overrightarrow{\textrm{OC}}+\overrightarrow{\textrm{OD}}}{3}\]

と表すことができます。

これで序文で与えられた２式から(1)で要求されている \(\overrightarrow{\textrm{OC}}\cdot\overrightarrow{\textrm{OD}}=0\) となることが分かるわけですが…

めぐろ塾の安田

(2)の２式のうち、前者は円のベクトル方程式であることは明白ですが、後者の式は有名な形ではありません。

\(\textrm{P}(x\:,\:y)\) として内積計算に持ち込まないとムリ
↓
座標平面に対応させるために、(1)から \(\textrm{C}(1\:,\:0)\:,\:\textrm{D}(0\:,\:1)\) とおく

部分の難易度は結構高いです。

めぐろ塾の安田

試験時間長いんだし、キレイな解答にこだわっちゃダメ！

\(\overrightarrow{\textrm{OA}}\) と \(\overrightarrow{\textrm{OB}}\) を基準としちゃっても、ガシガシ計算すれば(2)の前者の式の特徴までは解答できます。ここまでできてれば６割程度の点数はもらえて及第点でしょう。