2024上智理工【数学TEAP利用】解説・解答・講評

2024年4月1日2024年5月9日

2024上智大学理工学部のTEAPスコア利用方式の数学の解説・解答・講評をお届けします！

共通テスト併用方式の数学については↓の記事をご覧くださいm(_ _)m

１

問題

考え方

(1)は2024共通テストⅠＡまでの定番出題である「２変数１次不定方程式」を解くだけの問題。教科書ではユークリッド互除法で77と52の最大公約数を１と出す過程を遡りますが、解答のように小さい方の係数でくくってしまった方がカンタンです。

(2)はド・モアブルの定理を使うだけ。偏角の計算では、\(2\pi\) 周期性を意識して余りに注目しましょう。

(3)の(ⅰ)は、\(2^7=128\) を意識して対数法則で計算するだけ。

めぐろ塾の安田

(ⅱ)はムズいです。マーク式なんでテキト～に解いちゃいました(笑)

\(n^{100}<1.28^n\) の両辺の常用対数をとって、(ⅰ)を利用
↓
\(2^a≦n<2^{a+1}\) を使って、左辺を小さいものに、右辺を大きいものに変更
（\(n\) を消去）
↓
立式できた \(a\) の不等式を満たす整数 \(a\) の最小を求める

としましたが、指数グラフの増加が直線より強いってのを当たり前としちゃってるので、記述式の解答だと減点される可能性があります。

めぐろ塾の安田

厳密解答を作るとすれば、\(y=\displaystyle\frac{\log_{10}x}{x}\) って有名グラフの活用でしょうか？でも計算メンドくなるんで、マーク式だと解答の処理がベストだと思います。

解答

２

問題

考え方

上智大学が大好きな「空間」からの出題ですが、

空間ベクトルでは３つのベクトルを基準に考える

ことが徹底されている人であれば、解法に迷うことはないでしょう。

めぐろ塾の安田

めぐろ塾↓のベクトルの授業では毎週、黒板の左に必ず書くくらい大切！

日本全国どこからでも受講可能！
完全個別指導コースあり（オンラインも可）！
初回面談・初回授業は完全個別で無料（オンラインも可）！

めぐろ塾の安田

初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓

お問い合わせ

03-6841-7626

電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。

頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。

X（Twitter）のDMからのお問い合わせ

\(\overrightarrow{\textrm{OA}}=\overrightarrow{a}\) \(,\) \(\overrightarrow{\textrm{OB}}=\overrightarrow{b}\) \(,\) \(\overrightarrow{\textrm{OC}}=\overrightarrow{c}\) \(,\) \(\overrightarrow{\textrm{OD}}=\overrightarrow{d}\) が設定されていますが、\(\overrightarrow{d}\) が邪魔です。長方形（平行四辺形）って条件から、これを消去しましょう。 (1)がこの誘導になっています。

(2)は垂直条件を処理するだけ。

(3)は、

平面のベクトル方程式で、\(\overrightarrow{\textrm{OH}}=(1-s-t)\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}\) と表す
↓
ＯＨ⊥平面ＡＢＣ　を　\(\begin{equation}\begin{cases}\overrightarrow{\textrm{OH}}\cdot\overrightarrow{\textrm{AB}}=0\\\overrightarrow{\textrm{OH}}\cdot\overrightarrow{\textrm{AC}}=0\end{cases} \end{equation}\)　で処理して、\(s\:,\:t\) を確定
（平面との垂直は、平面を作る２ベクトルとの垂直で処理）

ってゆ～、

めぐろ塾の安田

オレ今年2024の解答速報で何回打ち込んだんだ？

ってレベルの有名処理。その結果から、

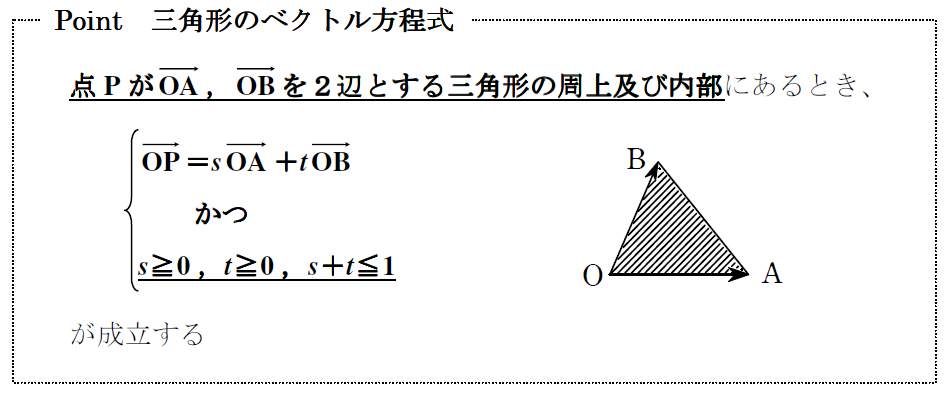
↑で点Ｈの位置が読み取れます。

(4)は、長方形の２辺の長さを、ベクトルの２乗からの内積計算２回で求めるだけ。

(5)は、(3)の結果を２乗して四角錐の高さを計算するだけ。

とゆ～ように、思考的には全く山場のない問題なんですが…

めぐろ塾の安田

計算メンドくせぇええええええええええええええええええええええええええええええええええー！！！

って受験者の皆様の気持ちを代弁して叫んでおきます(笑)

(4)や(5)がルートを含まない形での解答、ってことで計算ミスをある程度確認できる設計にはなっていますが、僕は一回では当てられませんでした…この問題を完答できれば、かなり合格に近づいたと思います。

解答

３

問題

考え方

(1)は微分して増減表作るだけ、絶対に落とせない！

(2)以降は、

「部分積分を思い付くか」が全て！

です。僕も10秒くらい戸惑ってしまいました。共テ併用の１(2)が同じような問題で、これを解いてなかったらもっと戸惑ったと思います。

めぐろ塾の安田

計算量も少ないので完答したい問題なんですが…受験者の半分くらいは(2)以降を落としてしまってるような気もします。

解答

４

問題

考え方

(1)は \(a_n=0\) 、(2)は(Ａ)に代入するだけ。

めぐろ塾の安田

ここまでは確実に解答してください。(3)は捨て問です。

３項間漸化式の形は(Ａ)で与えられている
↓
初項と第２項により(Ａ)を満たす数列は確定する
↓
初項と第２項を調整しやすいように、\(c_n\:,\:d_n\) の初項と第２項を０と１の組み合わせに

というのが全体的なストーリーですが、

(ⅰ)で \(c_n\) と \(d_n\) をもっと具体的に提示しなくていいの？
(ⅱ)の証明ってこれでいいの？

ってことで、設計が最悪な問題です。

まず前者ですが、僕は(Ａ)を満たす数列を式的に解析できないかでかなり時間使っちゃいました。\(a_{n+1}\) で割って２項間にするとか試しちゃいましたね、タイムロス。結局大手さんの解答も僕のと同じだったんで、多分大丈夫なんじゃないでしょうか？(笑)

めぐろ塾の安田

そして後者は…マジで良く分かんね～っす…

僕の解答も上智大学さん採点してくれませんかね？(笑)個人的にはこれでいい気がするんですが、大手さんは \(x_n=a_n-(sc_n+td_n)\) まで設定し、\(x_n=0\) を示して(1)と関連付けていました。個人的には感動しましたが、ここまで凡人の僕は思いつかないので、めぐろ塾の解答としては下記のものでいかせて頂きます。試験時間内にこれ解かされる受験生の皆さんに同情します…