2024九大【理系数学】解答速報

2024九州大学の理系数学の解答速報をお届けします！

〔１〕

問題

考え方

(1)は、ＰとＱが定点なので、直線のベクトル方程式で直線ＰＱ上の点を媒介変数表示し、これがＲと一致するのは \(a=-1\:,\:1\) のときって言って終了。ＰとＱが平面 \(y=1\) 上ってことに注目すればもっとカンタンにできると思いますが、こんな典型問題、考えるより手を動かしちゃった方が早いでしょう。

(2)は、

• ベクトルの三角形の面積公式を利用
• (1)の流れから、線分ＰＱを底辺として高さを計算

のどっちで三角形ＰＱＲの面積を \(a\) で表しても大丈夫です。計算量も大して変わりません、解答では後者でやっています。結局ルートの中が \(a\) の６次関数になりますが、\(a^2=b\) とおくと３次関数になるので、微分して増減表で最大値を求めましょう。

全体に凄く典型的な問題です。(2)辺りでの計算ミスはしょうがないですが、その場合に備えて丁寧な記述を心がけましょう。ほぼ完答はマストな問題です。

解答

〔２〕

問題

考え方

方程式 \(f(z)=0\) を見た瞬間に、条件反射で \(z^2-1\) をかけるってできないとアウトです。\(f(z)\) が等比数列の和って思って処理することもできますが、あまりに頻出処理なので。

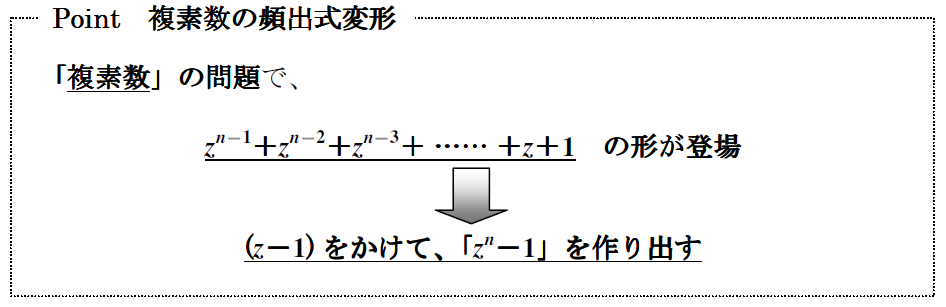
↑のようにめぐろ塾↓ではプリントで定型化しちゃうくらい頻出。

(1)はこれで \(f(z)=0\) から \(z^8=1\) を作ったら、両辺に絶対値をとって終了。

(2)は結構難しいですね。複素数平面上で、

\(f(z)=0\) の解は「１の８乗根」のうち、実軸上の２点を除いたもの
↓
\(wz\) で回転させて全て一致させるためには、
\(w=\cos 0+i\sin0\:,\:\cos\pi+i\sin\pi\)（０or \(\pi\) 回転させる）しかない

ってのがストーリーですが、ストーリーが読めても…

とか、どこまで論証すべきかを迷ってしまう問題。僕の解答も必要条件の論証が甘いので、減点されても文句の言えない解答になってしまっています。因みに大手さんの解答速報で、必要条件の処理をめちゃくちゃカッコ良く論証されているところがあって、個人的には感動しましたが…

と思って凡人が時間内で記述できる解答にさせて頂きました、それがめぐろ塾のモットー(笑)

(2)は、ストーリーが読めてたら論証不備での減点覚悟で結果を書きましょう。読めてなくても、「１のｎ乗根」の処理で \(f(z)=0\) の解を極形式表示するところまでを記述して部分点を拾うのはマストです。

解答

〔３〕

問題

考え方

ま～(1)は(2)・(3)のヒント設問なんで、テキトーに片付けましょう。解答では「大－小≧０」で片付けています。

(2)は、(1)で不等式が与えられていることから、整数問題の常套解法である範囲の「絞り込み」を行うことは明白です。階乗が題材の問題は頻出ではありませんが、整数問題の「絞り込み」に慣れている人であれば解法に迷うことはないでしょう。\(b\) の範囲を「絞り込み」ます。

(3)も同様に、

\(a=b=c\) のときは当たり前に成立
↓
それ以外のとき、与等式の \(a\) と \(b\) の対称性から、\(a<b\) として良い
↓
「平均」の意識を持つと、与等式から \(a<c<b\) が分かる
↓
(1)を使った \(b\) の範囲の「絞り込み」で、\(a<c<b\) の場合は不適と言える

というのがストーリーで、整数問題の常套処理ばかりで完結できる良問です。でも一つ一つの論証に点数がしっかり入ると思いますし…前述の通り階乗が題材の問題は頻出ではないので、完璧に解答できた人は少なそう。完答できずとも、\(a<b\) とする部分くらいまでは記述し、部分点は拾ってください。

解答

〔４〕

問題

考え方

見た目…

って思いましたが、冷静に見るとｎが最大で５にしかならない。ただ数えるだけのサービス問題です。しかも、斜め直線のカウントが入るのもｎ＝５のみというサービス仕様。完答はマストな問題でしょう。

解答では(3)の斜め直線を、ダブりが起きないように中点に注目してカッコよくカウントしましたが、こんなのできなくていいです。愚直に数えて、答を当てましょう。

解答

〔５〕

問題

考え方

題材としては、

(1)で２変数の「定積分数列」の漸化式を部分積分法で立式
↓
(2)で、立式した漸化式を用いて極限を考える

という典型内容なんですが、受験者の出来はあまり良くない気がします。

• 被積分関数が２つの積での出題がほとんどなのに、今回は３つの積
• (2)では、ｎだけを \(\infty\) に飛ばすので、ｍは定数（有限確定値）扱いしなきゃダメ
• なのに漸化式でｍがずれててウザい

僕も最後で結構ハマってしまって…最初こんな解答↓を打ち込んでしまいました。

って感じで(笑)ほんで後発特権で他の解答速報さんで答え合わせしたら…

って気づいて凹む…流石に解答見る人を混乱させるのはまずいので、本解答はこれで打ち込ませて頂きました。上のダメ解答は、

って癒されるためにお使いください、減点喰らう解答ではないんですけどね…参考にはしないでください(笑)

３つの積のため、(1)もカンタンではありませんが、

• 部分積分法において \(e^x\) は積分方向に採用
• \(m+1\) を \(m\) に、\(n+1\) を \(n\) にずらしたいから、\(x^{m+1}(\log x)^{n+1}\) はまとめて微分方向に採用（積の微分法利用）

というように、部分積分法の基本をしっかりと意識すれば解答できるでしょう。(1)までできていれば及第点だと思います。

解答

講評

昨年2023の解説記事も作成しましたが↓

これと比べると…

です。大幅に難易度が下がりました。ま～昨年が異常に難しかったので、例年通りに戻ったと言うのが正しいかもしれません。

まず、2022・2023で出題されていた共通テストよろしくな長文問題が姿を消しました。九大のトレンドになっちゃうのかな～っと思っていたので、これがなくなったのは受験生の皆さんと同じく大歓迎です、去年問題文打ち込むのが凄い大変だったので(笑)

このことと、去年2023より計算量・難易度が大幅に下がったことを考えると、合格最低点はかなり上がるでしょう。

合格には、　１のほぼ完答　＋　２(1)　＋　３(2)まで　＋　４完答　はマスト！

に思えます。医学部医学科だと、これに＋大問１つ分くらいの点数は欲しいところです。

これで今年度の受験は終わりって人、本当に一年間お疲れ様でしたm(_ _)m

国公立後期を受験する予定の人は、それに向けて気を抜かずに勉強頑張って！！

今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！

君の大学受験が最高の結果になることを祈ってます！