2024共通テスト数学ⅠＡ解説
2024大学入学共通テスト数学ⅠＡの解説を速報します！
めぐろ塾の安田数学ⅡＢについては↓の記事をご覧くださいm(_ _)m
第１問（必答問題）
問題（クリックすると表示されます）
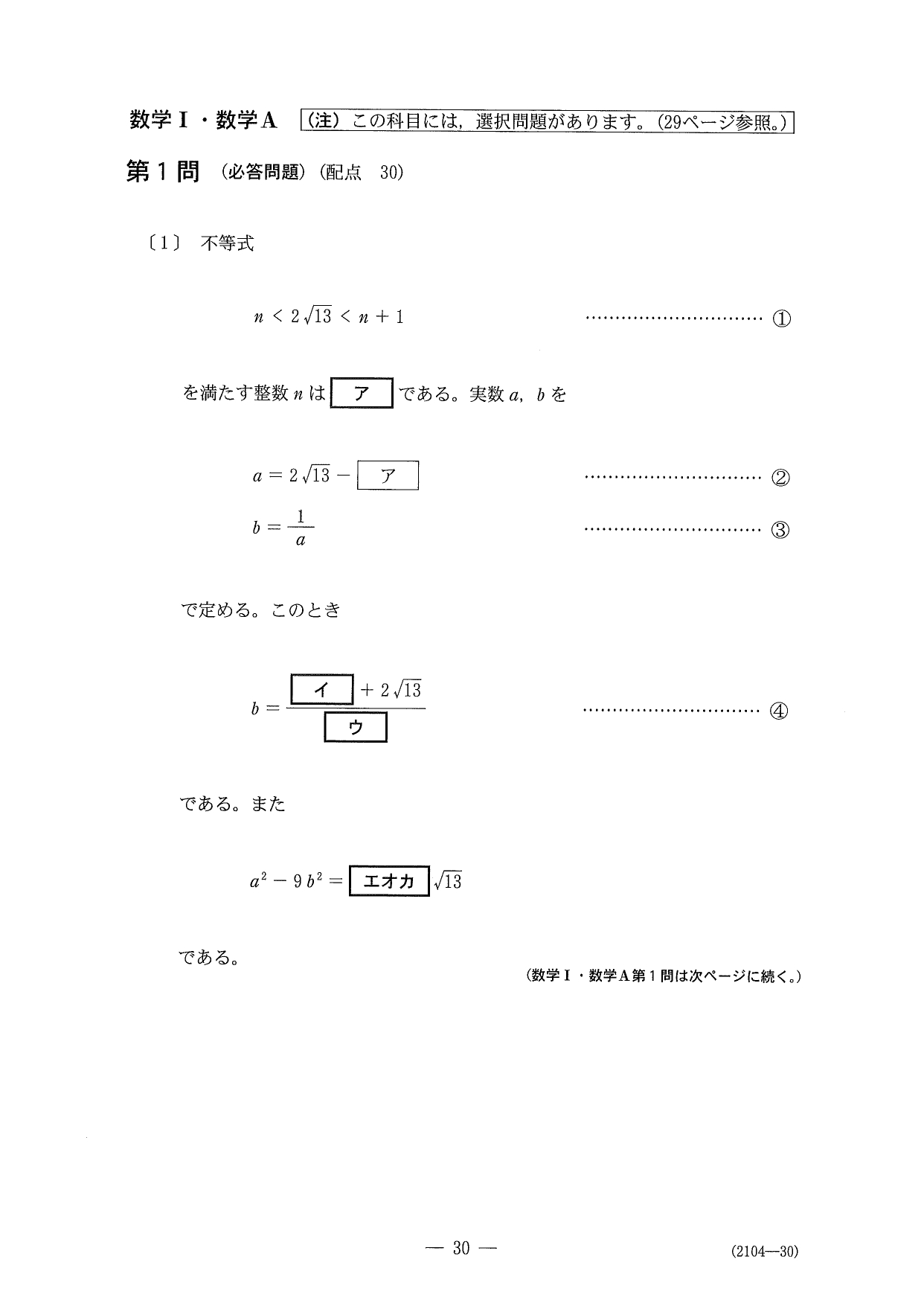
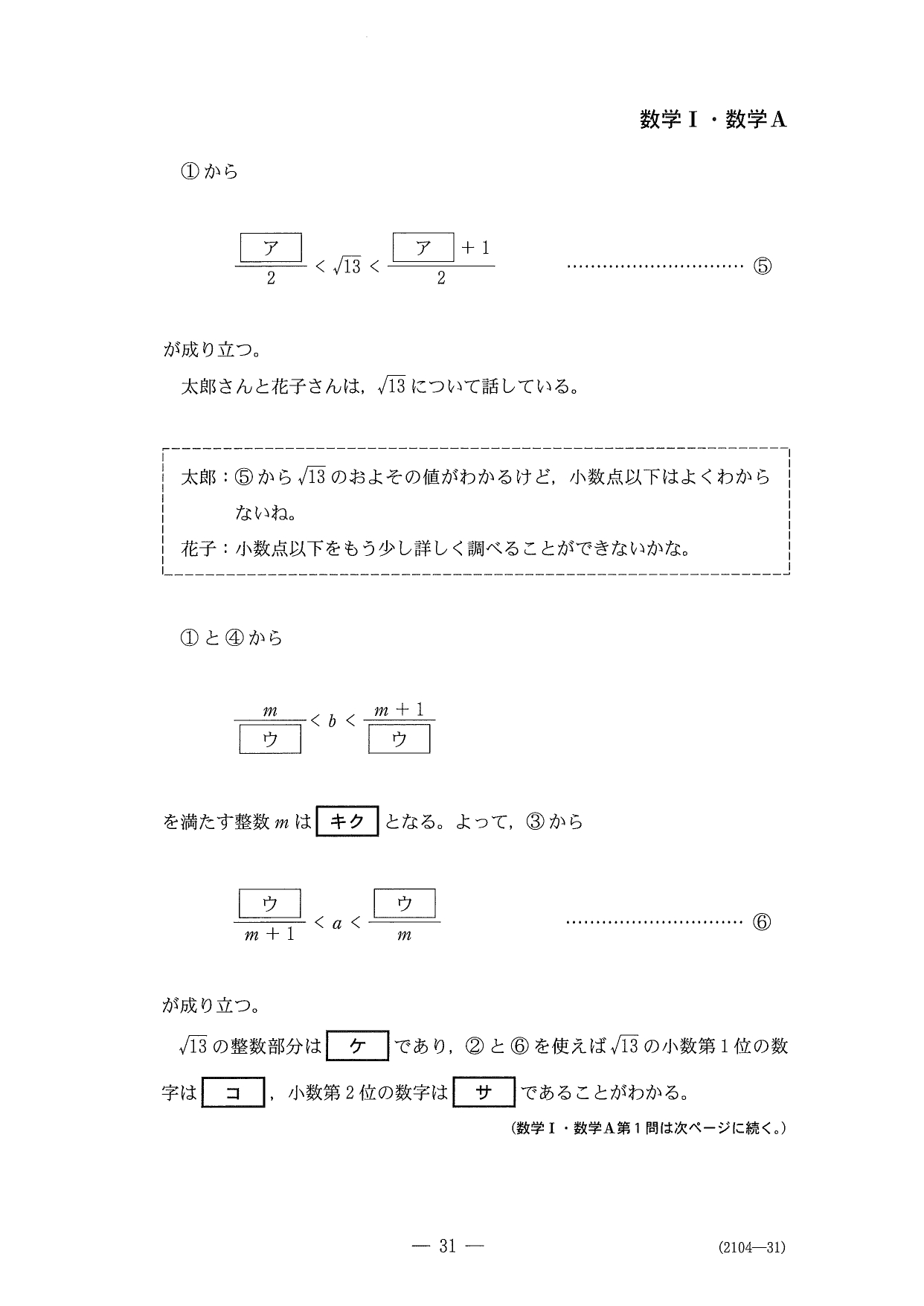
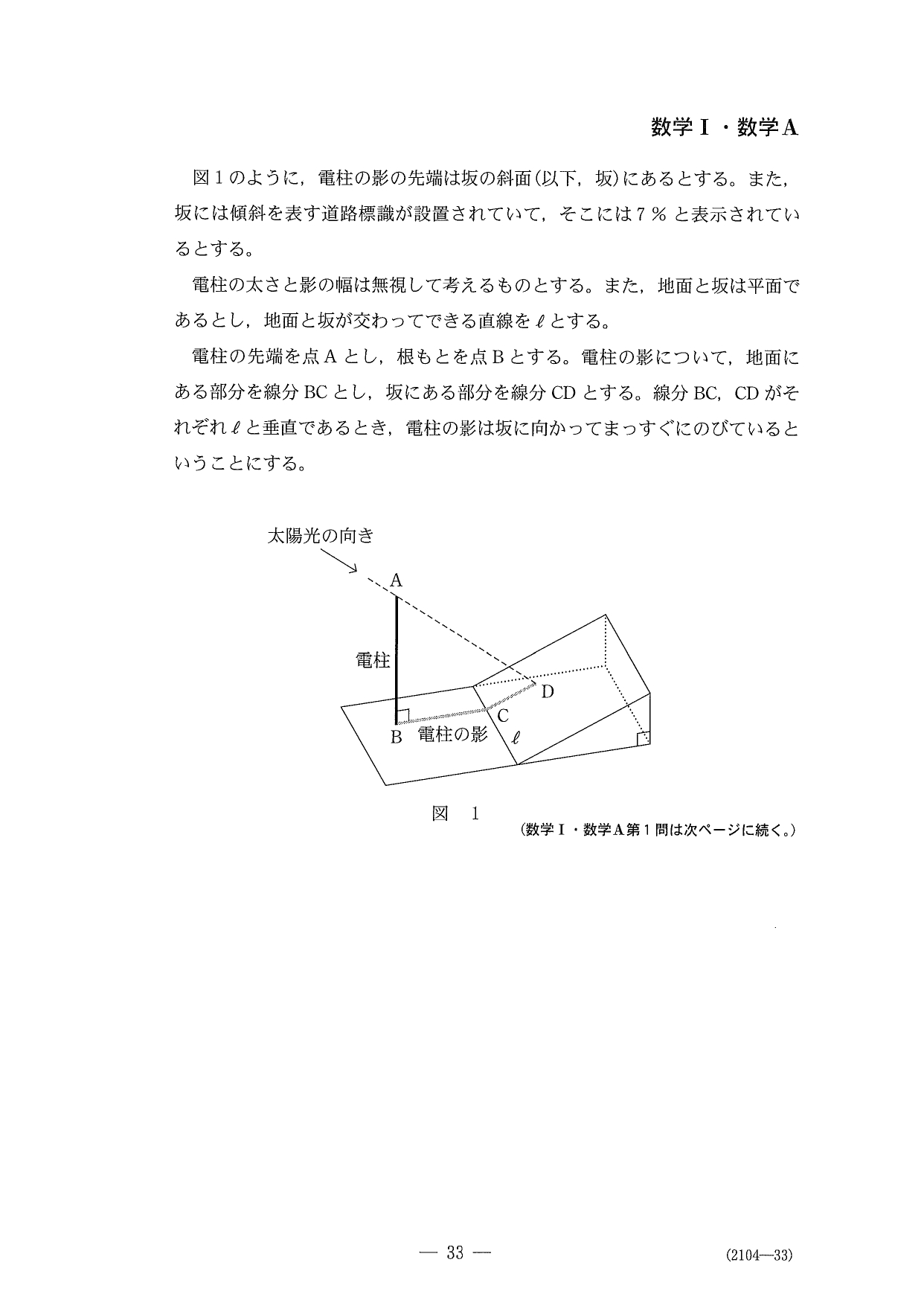
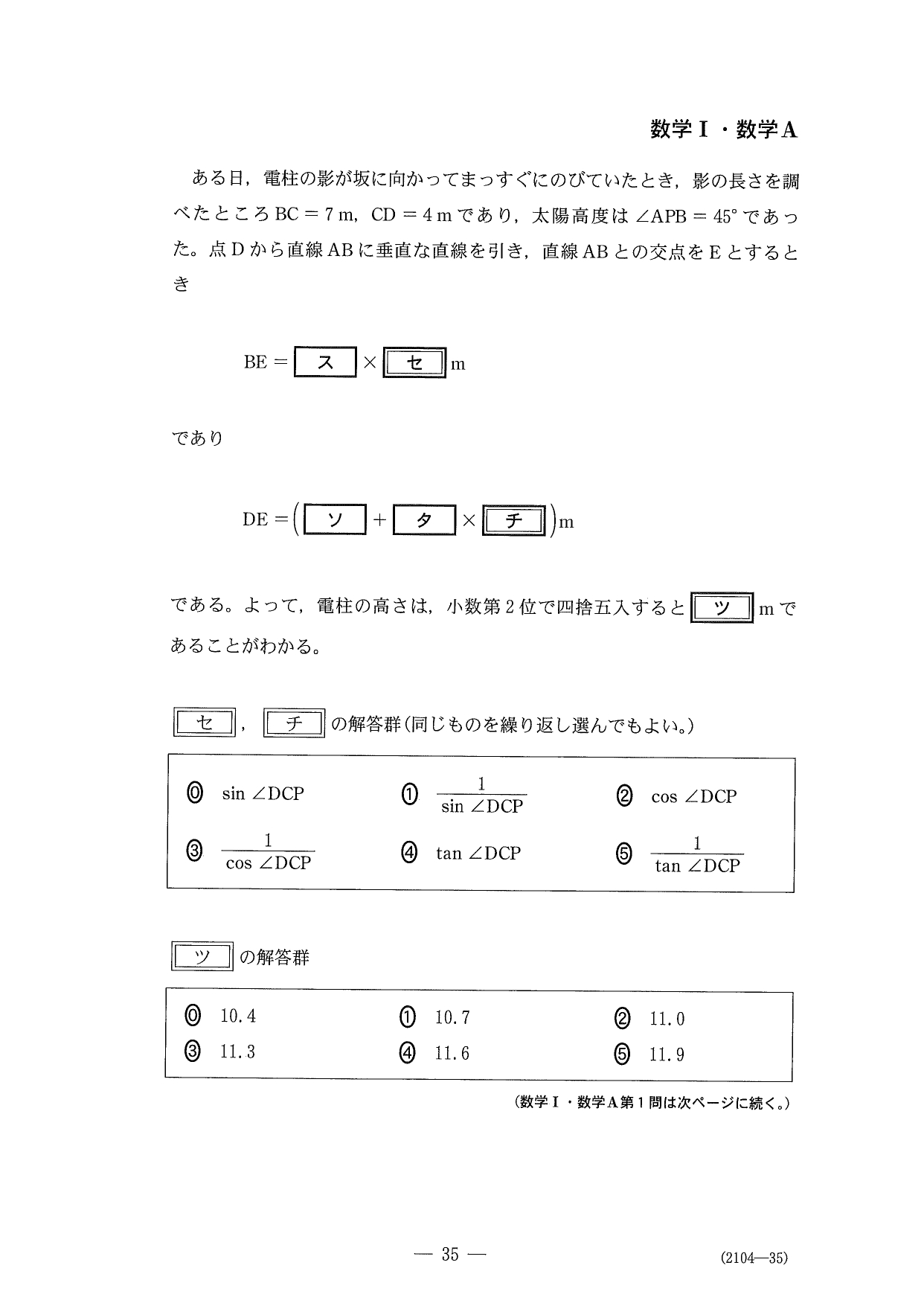
解答
第２問（必答問題）
問題（クリックすると表示されます）
解答
第３問（選択問題）
問題（クリックすると表示されます）
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答
第４問（選択問題）
問題（クリックすると表示されます）
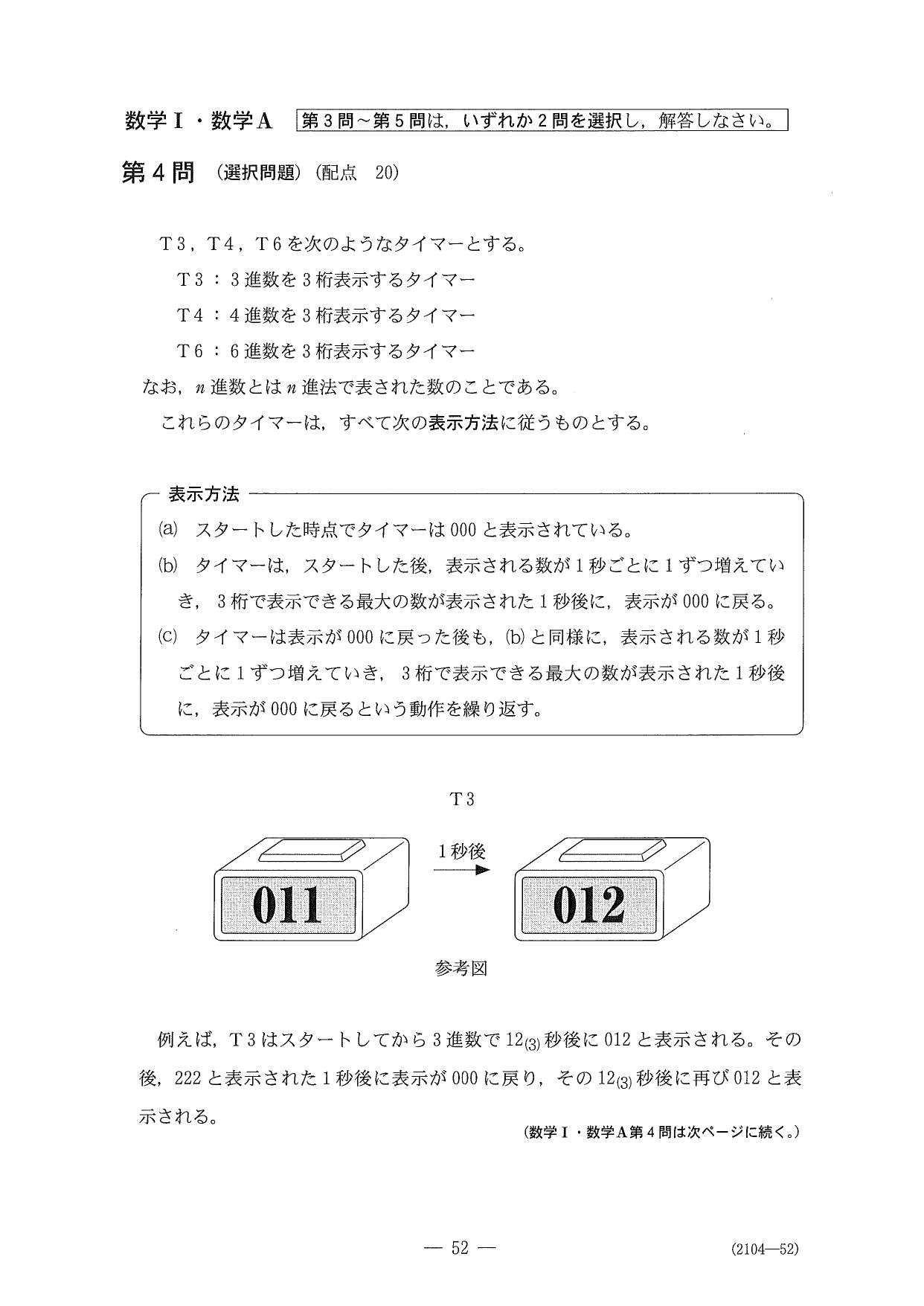
解答
第５問（選択問題）
問題（クリックすると表示されます）
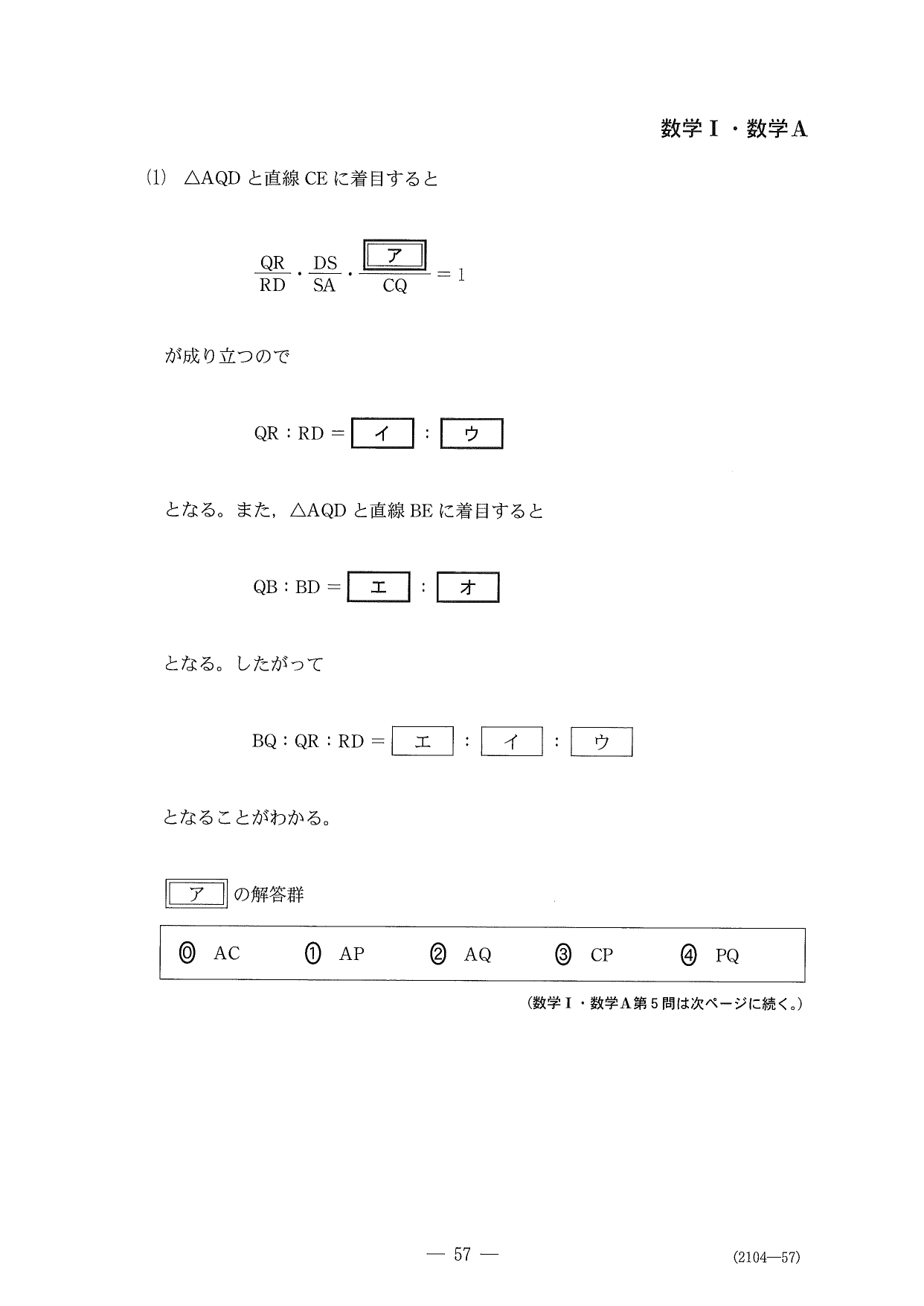
解答
講評
めぐろ塾の安田僕は第３・４問を選択し、解答を打ち込む前に時間測って解きましたが…個人的には2023に比べて…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式 | 70分 | ４問 （第３～５問は、２問を選択して解答） | やや難化 |
に感じました。
第１問
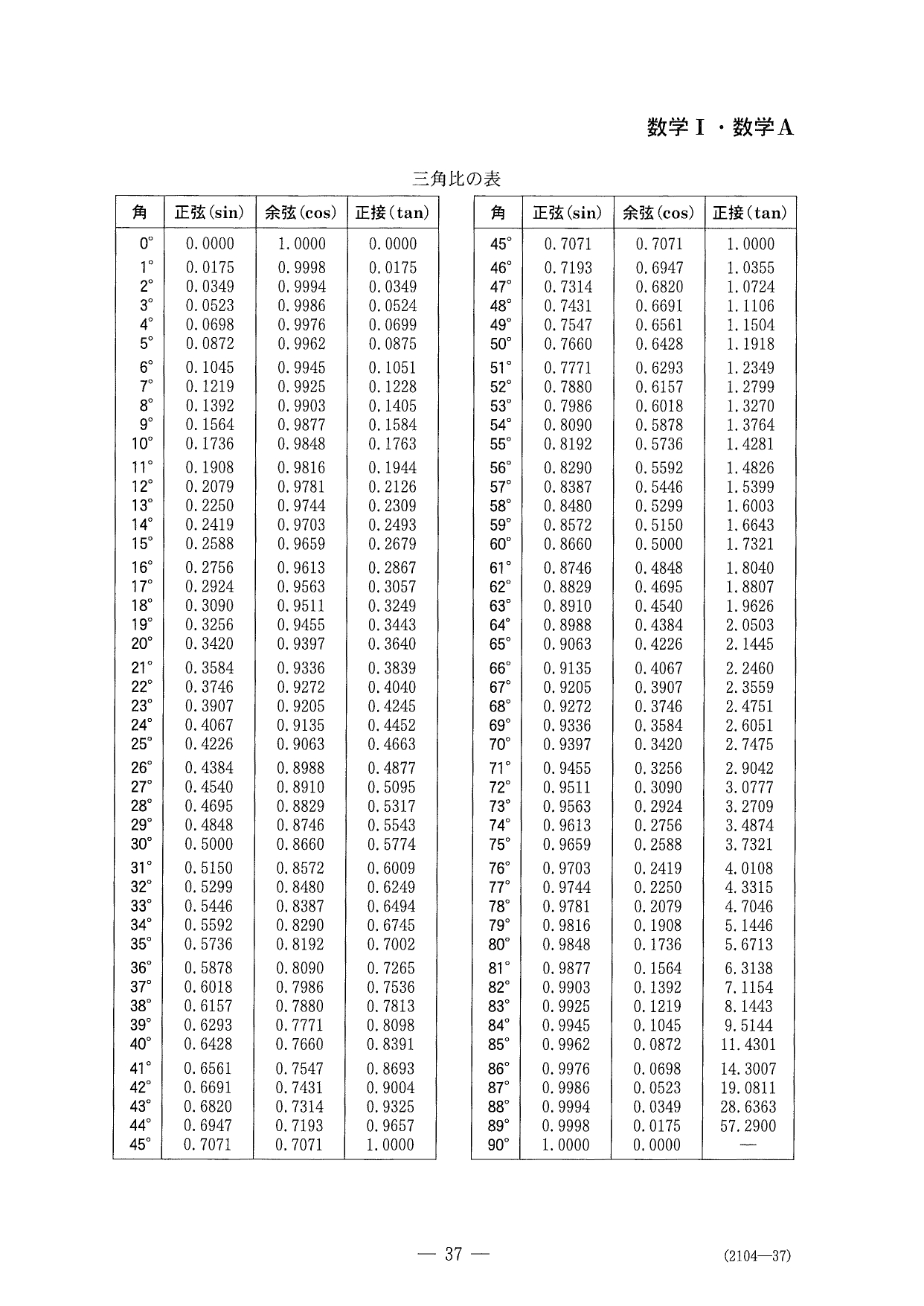
〔１〕は有理化、整数部、小数部についての問題で、解きやすいと思います。
〔２〕も中盤まではカンタンなんですが…
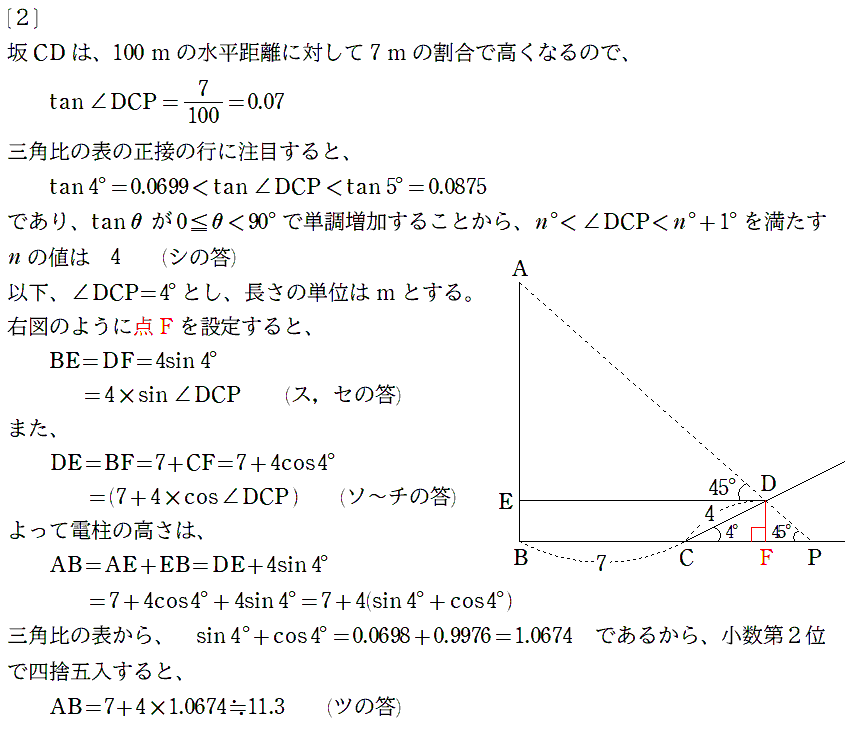
めぐろ塾の安田最後の設問がヤバイっす…混乱して、これだけで10分以上使っちゃいましたorz
冷静にＡＥやＥＢを \(x\) とおいて、ＣＤと \(x\) の連立方程式を作成
↓
\(x\) を消去し、ＣＤについて整理
するだけなんですが、
- 直接ＣＤ＝…を作れるんじゃないかと思っちゃう
- 「∠ＤＣＰの大きさは、ちょうど４°とする」ってしてるのに、この選択肢では∠ＤＣＰが使われててイライラする
ってことで、個人的にはトラウマな問題(笑)僕のように下手に時間を使ってしまうより、バッサリ捨ててしまった方が良いかもしれません。この問題のせいで、僕はこの後チョー焦って解くことになってしまいましたorz
第２問
〔１〕は、
三角形ＰＢＱの面積を時刻 \(t\) の２次関数で表す
↓
\(0≦t≦3\) と \(3<t≦6\) で場合分けが発生
↓
最大・最小と不等式を考える
という、文章量も多くない、典型的な構成です。計算量は多いですが…
めぐろ塾の安田「２次関数がそろそろくるでしょ～」って思えてた人は有利です！
因みに△ＰＢＱの面積を計算するのに、解答ではこの公式を使っちゃってるんですが…
この公式ってⅡＢ範囲だから、ⅠＡで使うのまずくない？
って先輩に突っ込まれました(笑)台形から三角形３枚を引くってするのが出題者の求めてる解答っぽいですね、共テのプレテストでもそーゆー解法を使う問題が出題されていたので。
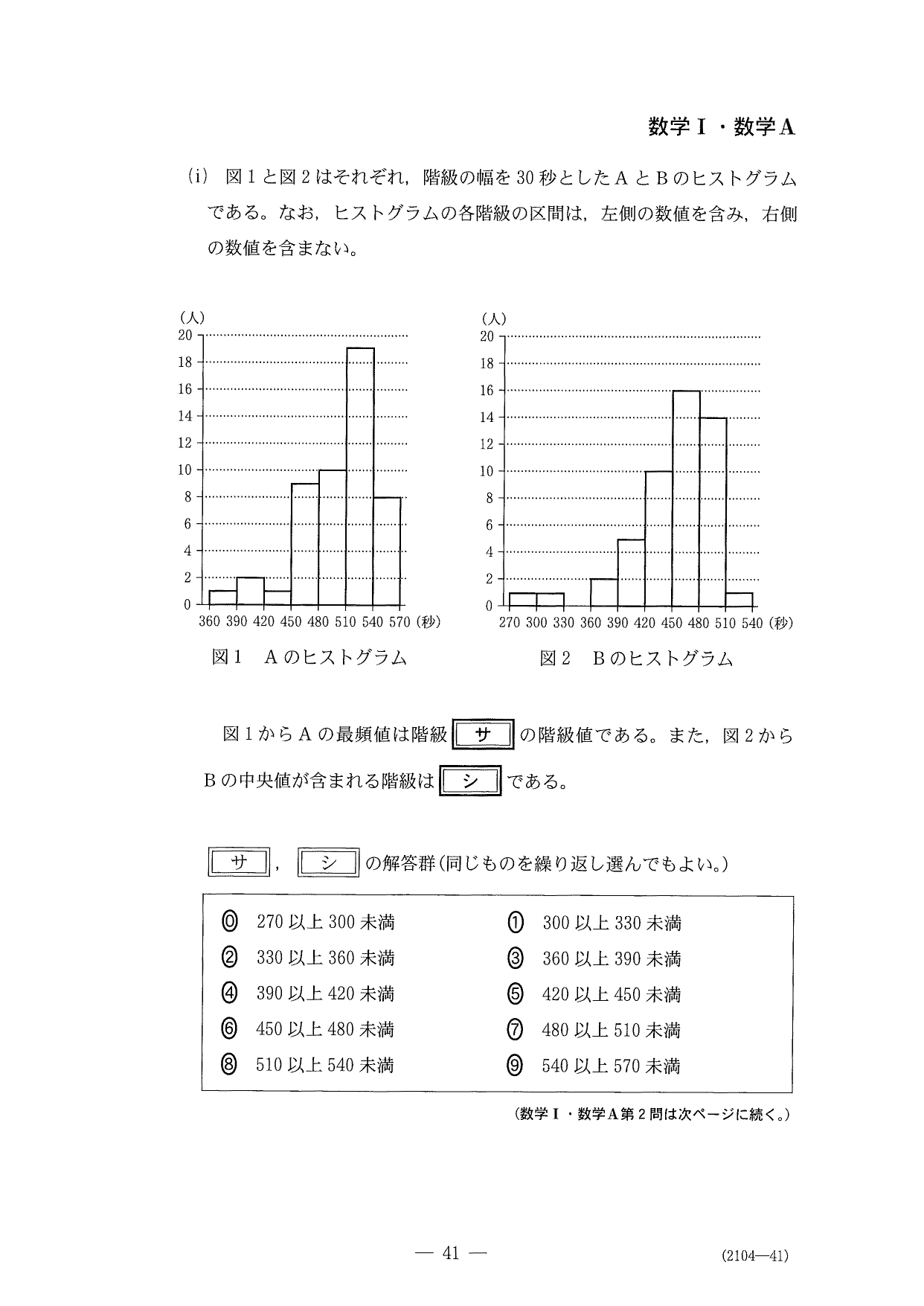
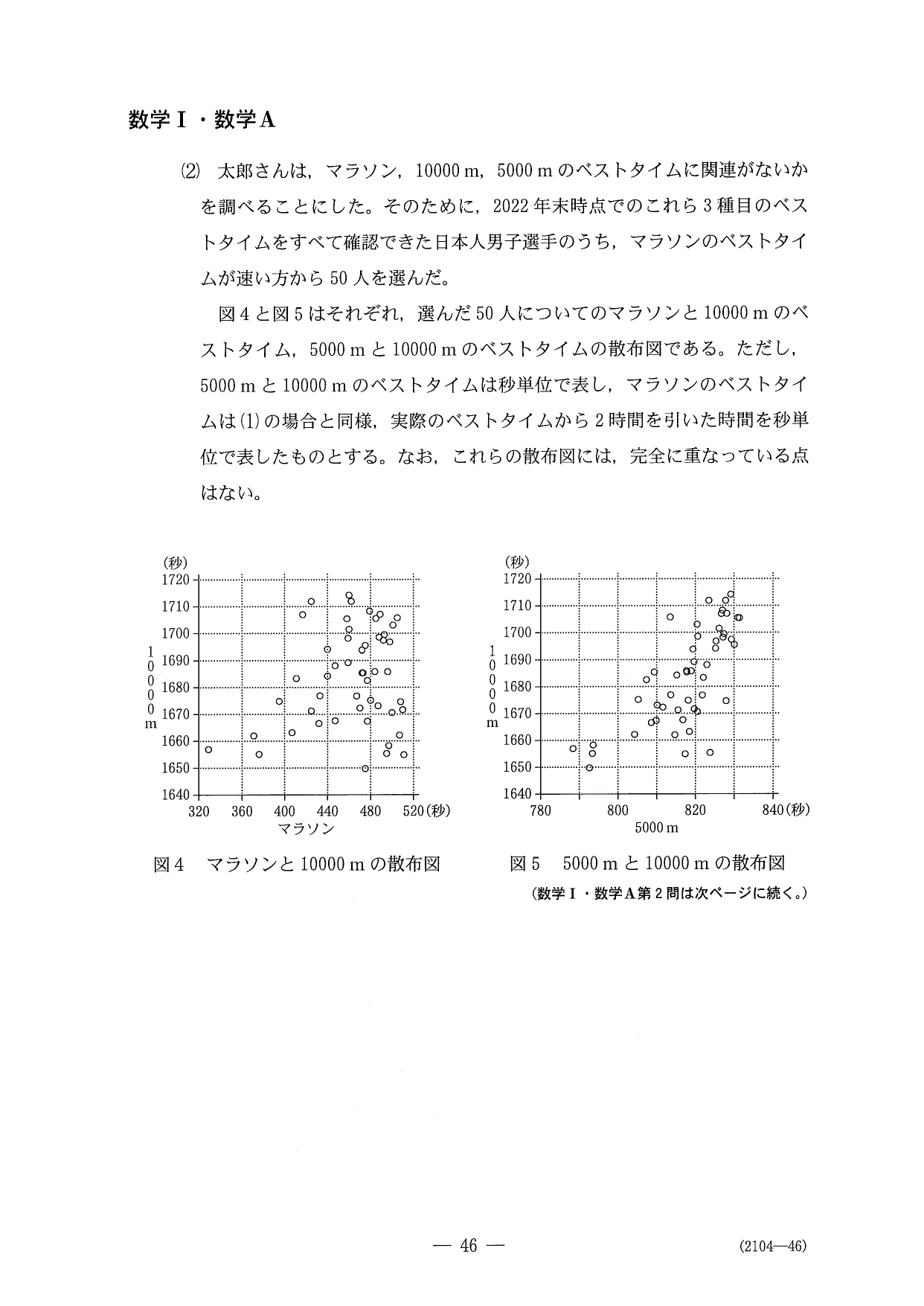
〔２〕はデータの分析で、去年に引き続き難易度は低めでした。ただ…
めぐろ塾の安田「セ」の四分位範囲の差の絶対値の出題がビミョー…
箱ひげ図からの目視でテキトーにやっちゃっていいのか、ヒストグラムまで遡って厳密に式で考えるべきなのか、少し迷っちゃいました(笑)P42の「図３より次のことが読み取れる」って文章を受け取って、解答では前者でやっています。
第３問
去年に引き続き、条件付き確率が出題されませんでした。そもそも去年は「場合の数」のみで「確率」も出題されていませんでしたが。
誘導が親切なので、それに従って計算していくだけですが…
めぐろ塾の安田鬼門になるのは(2)の最後（サ、シ）と(3)の最後（チ～ナ）
(2)の最後は、それまでの誘導に従うのではなく、自力で、
３種類のうち１～４回が２種類だけで、１種類はダメ → \({}_3\textrm{C}_2\)(\(2^4\)－\(2\))
という有名処理に気づかないといけません。そして(3)の最後でこれを使います。ま～この２つは外しちゃってもいいかもしれません。その場合も(3)の前半２問は取れるので、ここの点数は確保しましょう。
第４問
前半は珍しく「ｎ進法」、後半ではお決まりの「２変数１次不定方程式」を解かせる問題でした。計算量も多くなく、去年と比べてもカンタンです。
因みに解答では、
\(27a-64b=1\) を解くのに、\(27\) でくくる
手法をとっています。教科書の多くは \(27\) と \(64\) の最小公倍数１をユークリッド互除法で求める過程を遡りますが、こっちの方がカンタンです。知らなかった人はこれを機に覚えておきましょう。
めぐろ塾の安田因みに僕は第１問で時間使い過ぎたせいで…第４問を10分弱で解く時間しかなく…最後を当てカンで埋めるしかなくなって…外しました(笑)
最後も別に難しくはありません。式を立てると「偶数＝奇数」になっちゃっておかしい、という整数問題のお決まり処理です。
第５問
去年の解説記事でも言ってるんですが…これは選択しない方が良かったんじゃないでしょうか？去年の問題よりはカンタンで、例年通り「メネラウスの定理」と「方べきの定理」を使う問題に戻りましたが…
めぐろ塾の安田まず、前半。「メネラウスの定理」で注目するキツネが探しにくい…
「メネラウスの定理」は、以下のように、
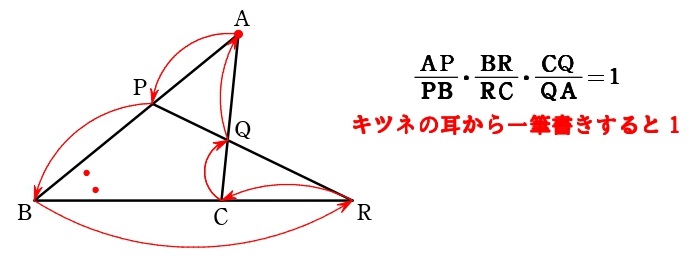
とおさえている人が多いと思いますが…この問題…星形なんでキツネがたくさんいすぎて、どのキツネに注目するのかが分かりにくいです。解答では注目するキツネに色をつけておきましたが…
めぐろ塾の安田僕は結構混乱しました。しかも最初耳から始めてくれてないし(笑)
さらに、後半。これはセンター試験最後半からの「図形の性質」の出題でのお決まりではありますが、
問題途中で円が導入されるので、円を作図せずに「方べきの定理」が使えないとアウト
です。
めぐろ塾の安田こーゆ～のって共通テストでしか出題されません。めぐろ塾では一応トレーニングさせます↓
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答では同一円周上の点に色をつけて分かりやすくしたつもりですが…これでも
分かりにくい
って思う人は絶対にこの問題を選択しない方がいいですね(笑)
総評
総じて言って、「必答問題はやや難化、選択問題はやや易化」だと思います。ただ…
- 第１問の最後の設問がヤバイ
- 第２問の最初も、典型的だけど計算量は多い
とゆ～、前半で時間を消費させてしまう構成になっているため、満点狙いにいっちゃうと去年より難化と言えるでしょう。
めぐろ塾の安田バッサリ第１問の最後の設問を捨てた人は、「変化なし」か「やや易化」に思えるんではないでしょうか？因みにプロ講師である僕の点数は…
- 第３問の一番最後をフツーに間違える…－２点
- 第４問の最初でケタの見間違え… －５点
- 時間なくて第４問の最後は当てカン、見事に外す… －３点
で90点…
易化したはずの選択問題でボコボコ間違えることになってしまいました(笑)
でもお互いに切り替えましょう！
もう共テのことは忘れて私大に向けて勉強だっ！！
僕も解答速報で君たちと一緒に戦います(笑)
なお、本年は速報性を重視した記事にさせて頂きました。この記事を見ている高２生とかで、共テの詳しいテクニックとかを知りたい人は2023の記事↓をご参照くださいm(_ _)m
また、今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
