2024共通テスト数学ⅡＢ解説
2024大学入学共通テスト数学ⅡＢの解説を速報します！
めぐろ塾の安田数学ⅠＡについては↓の記事をご覧くださいm(_ _)m
第１問（必答問題30点）
問題（クリックすると表示されます）
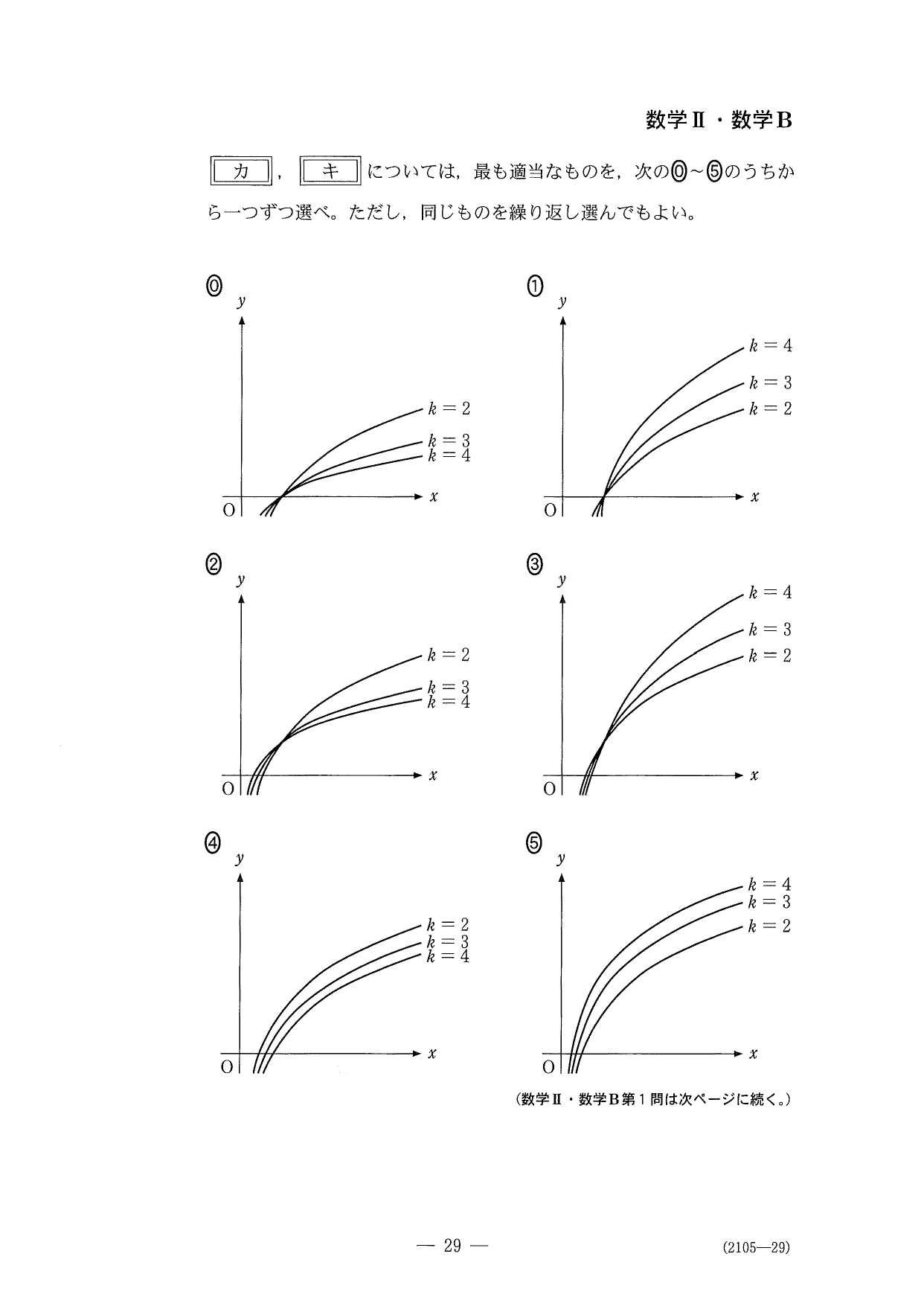
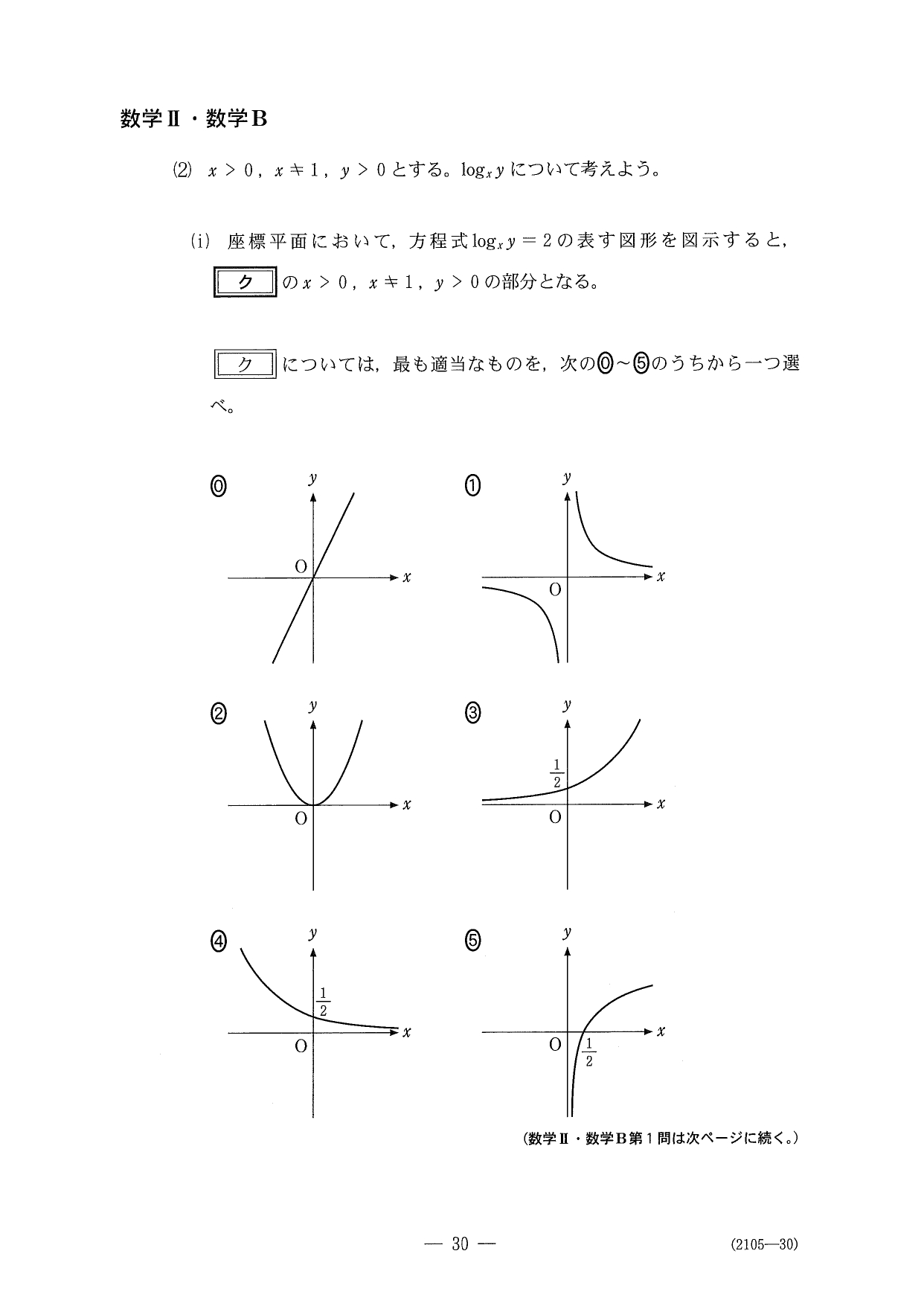
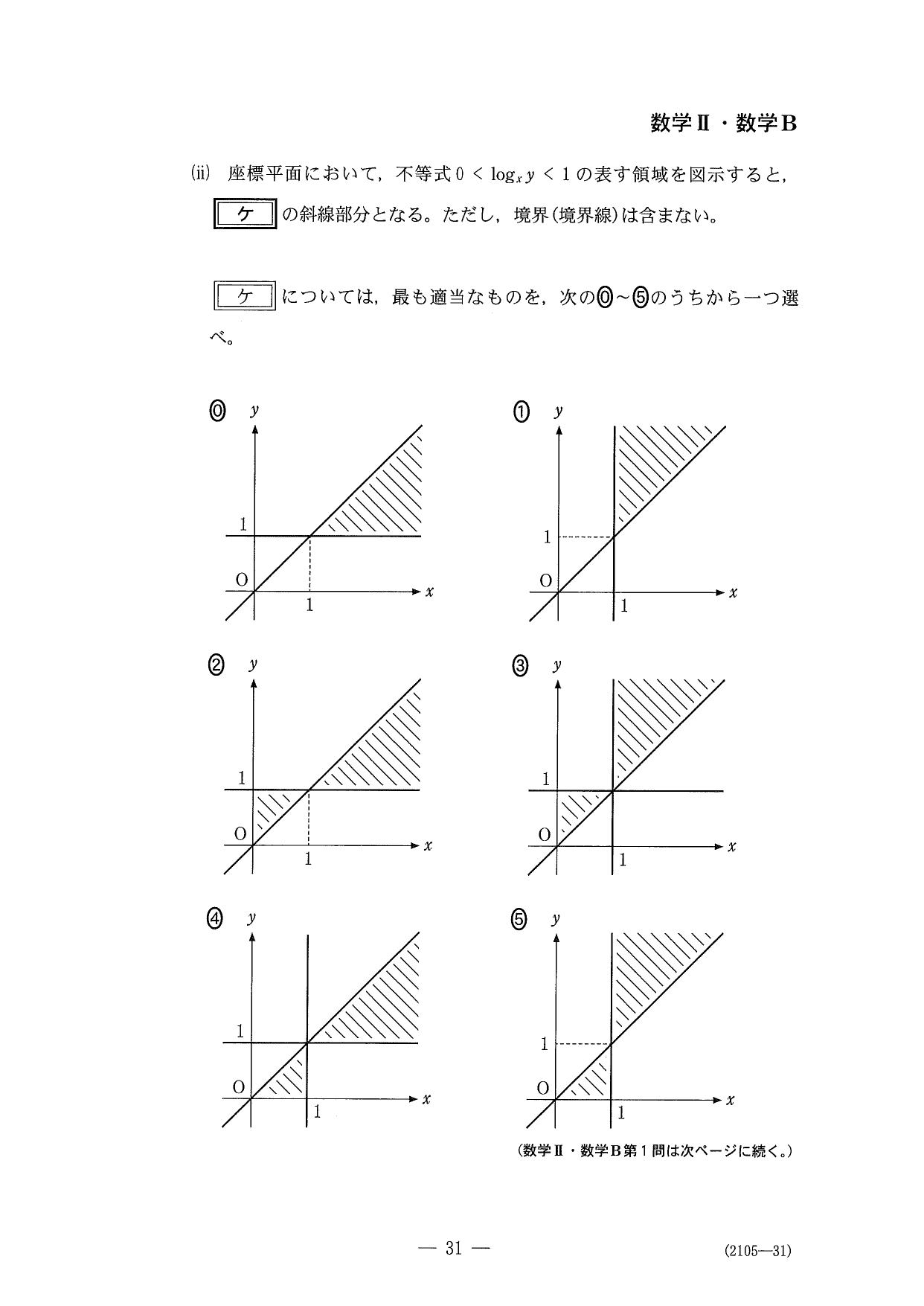
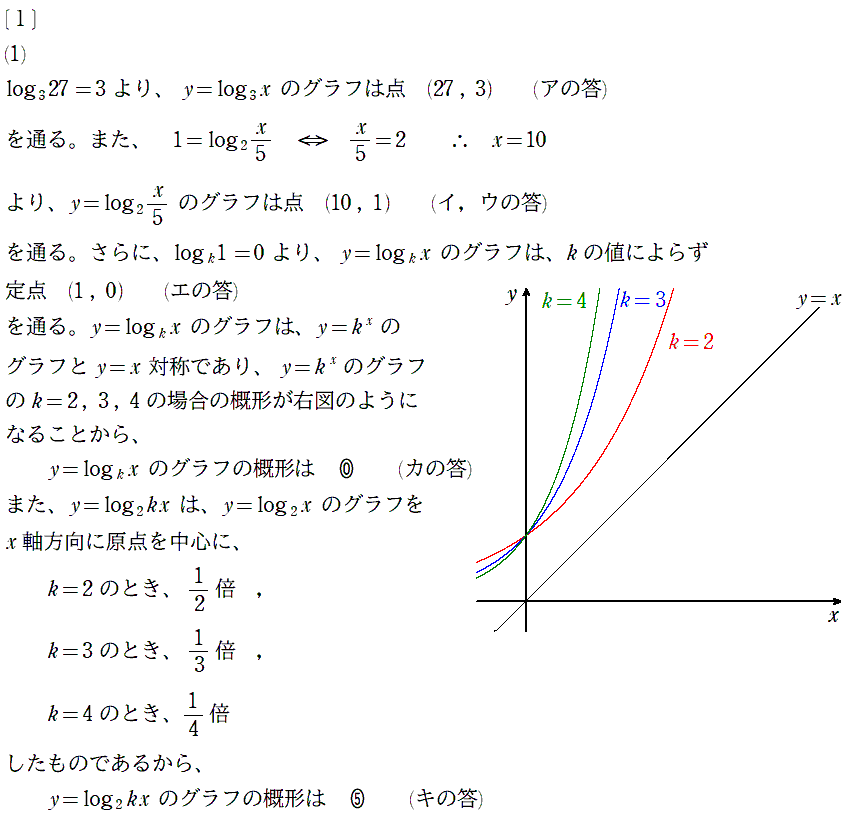
解答
第２問（必答問題30点）
問題（クリックすると表示されます）
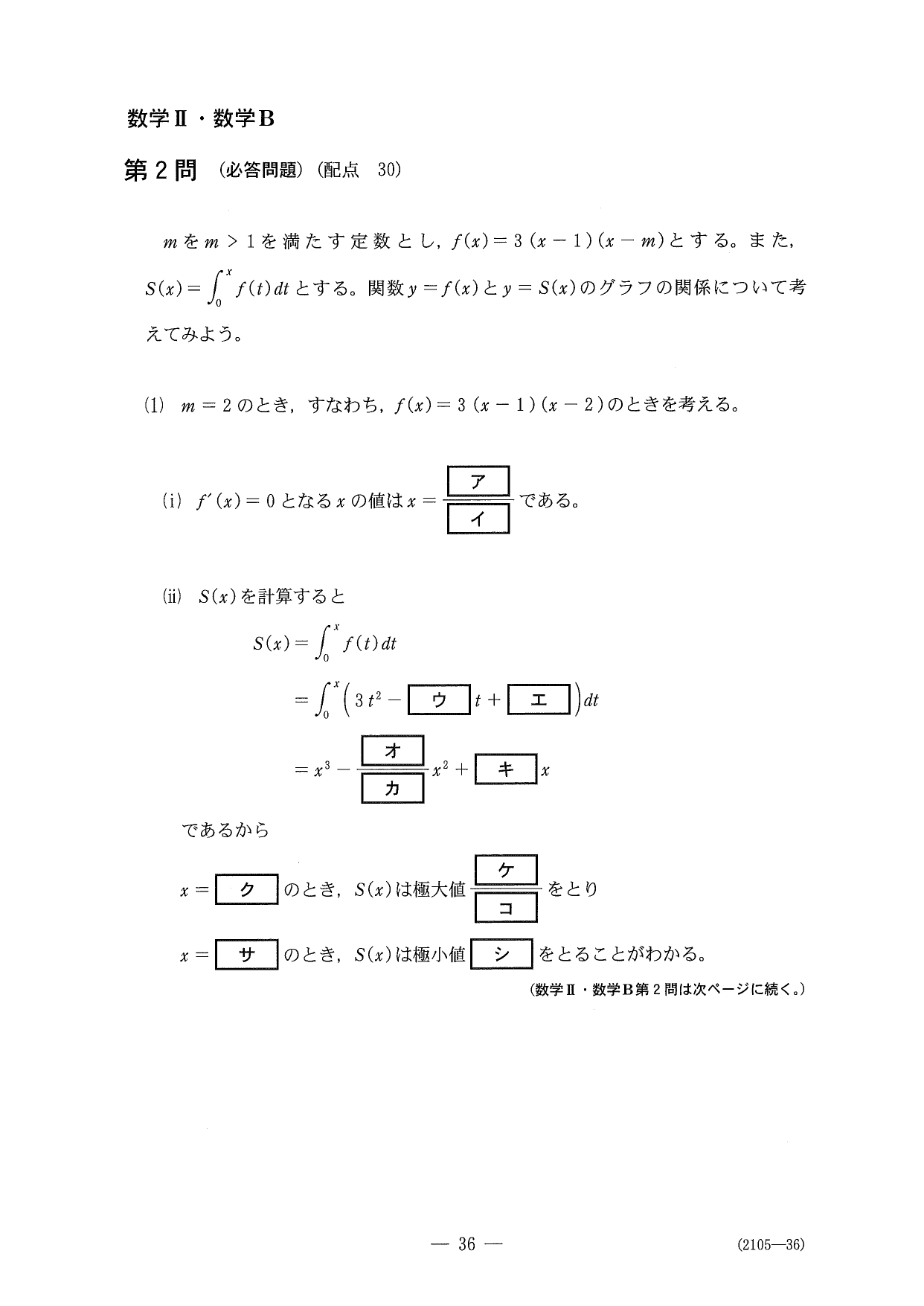
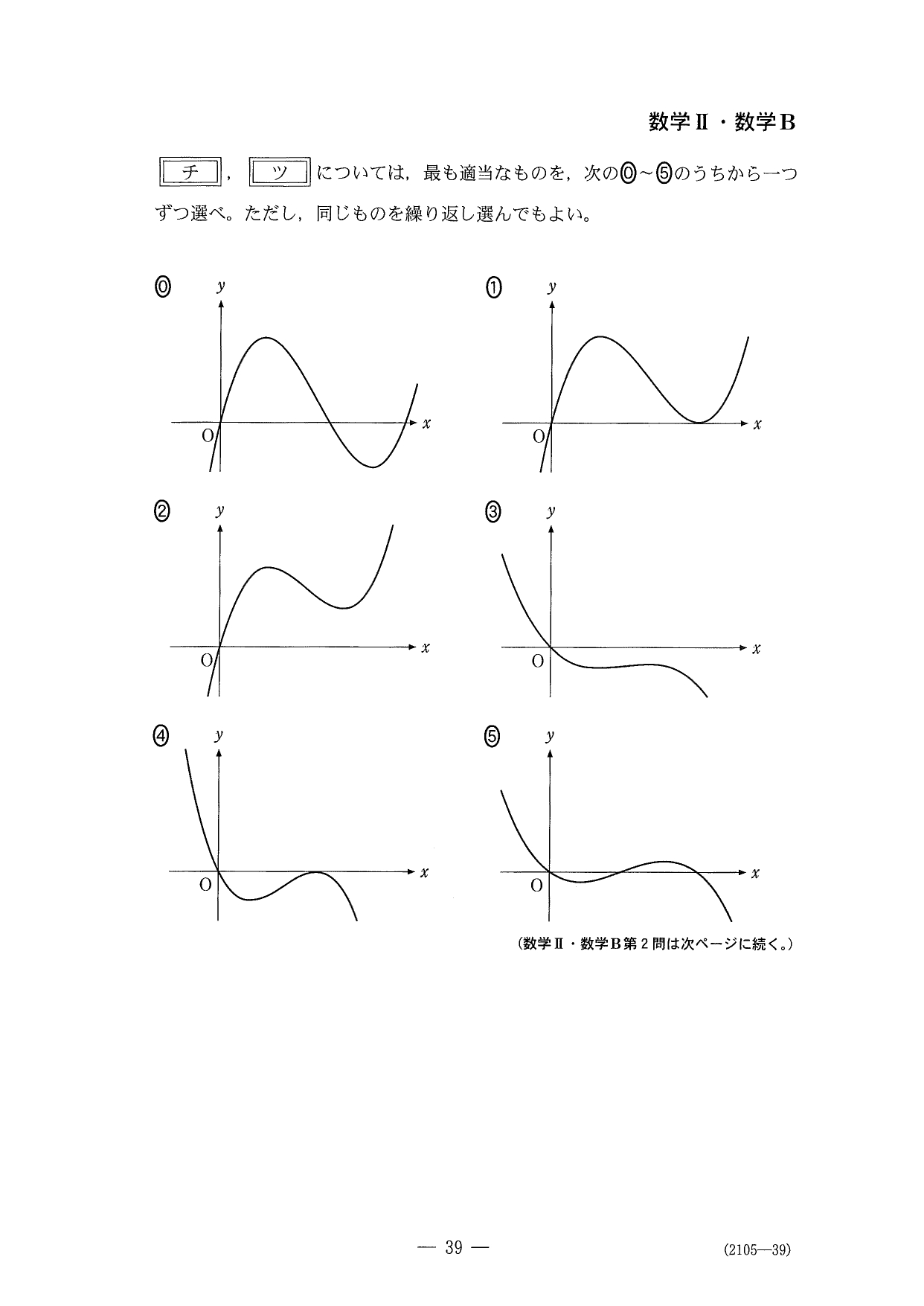
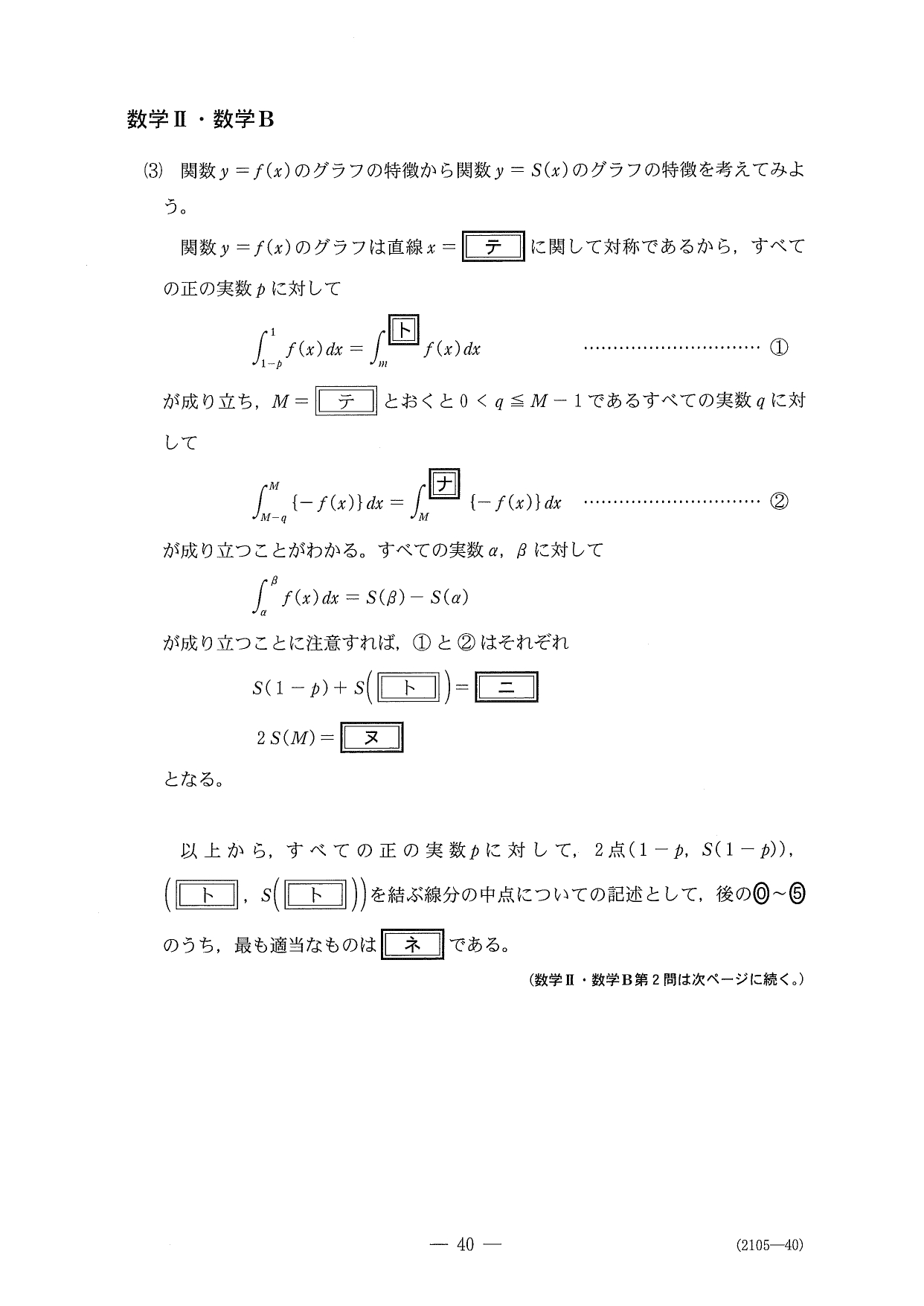
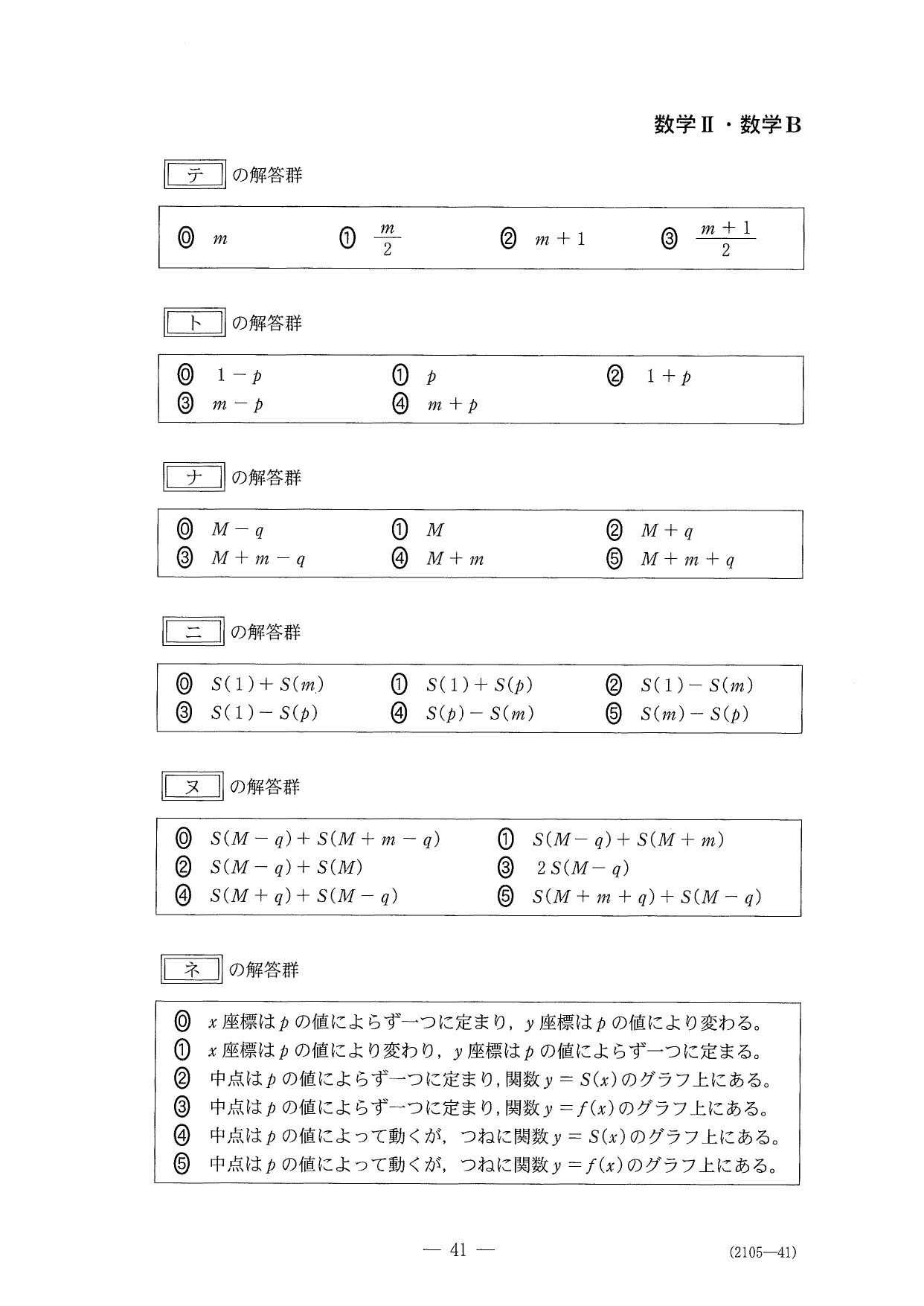
解答
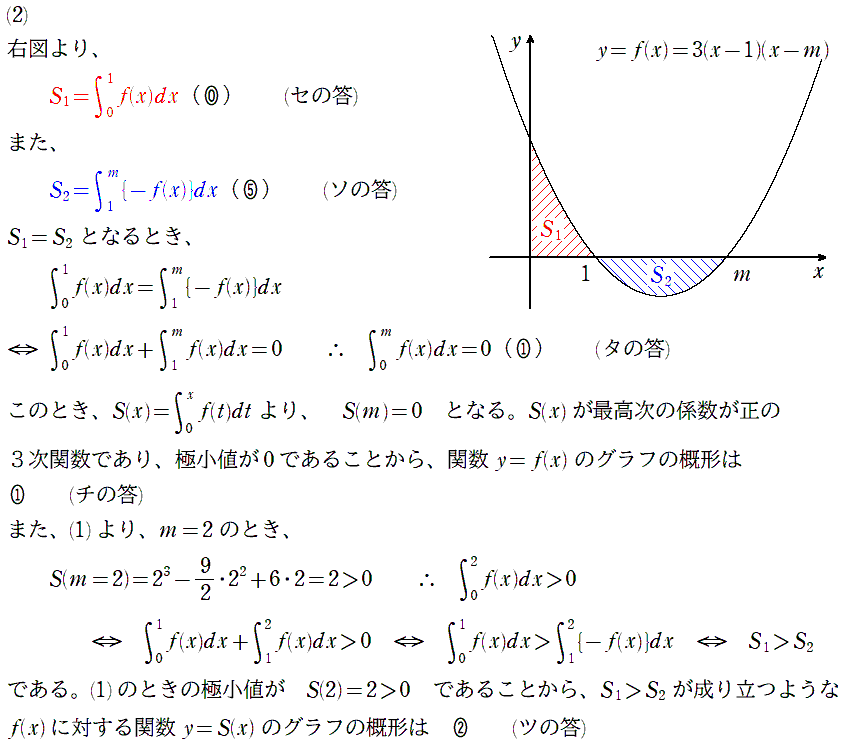
第３問（選択問題20点）
問題（クリックすると表示されます）
解答
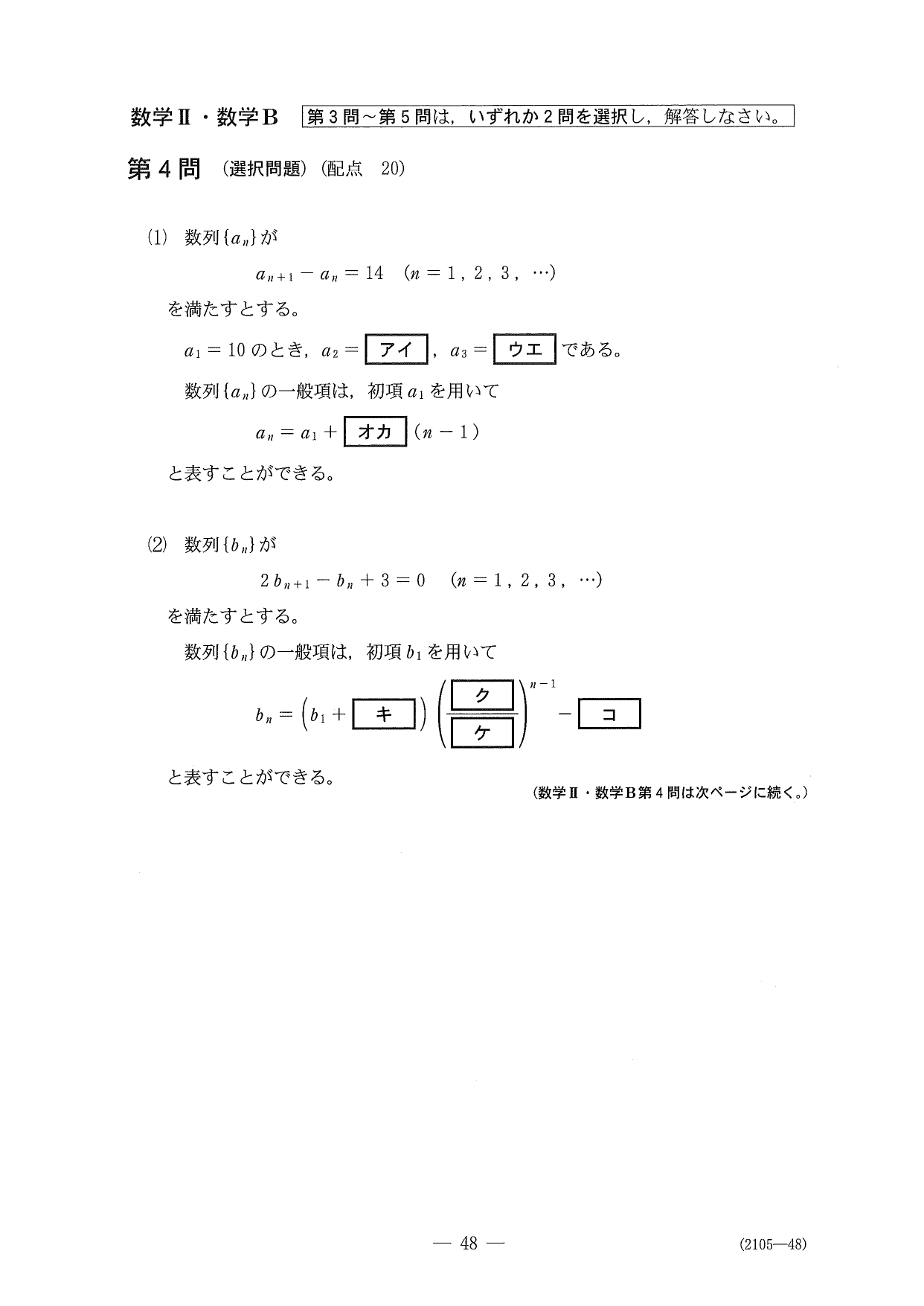
第４問（選択問題20点）
問題（クリックすると表示されます）
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答
第５問（選択問題20点）
問題（クリックすると表示されます）
解答
講評
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式 | 60分 | ４問 （第３～５問は、２問を選択して解答） | 変化なし |
第１問
めぐろ塾の安田今年は「三角関数」が出題されませんでした！
〔１〕は「指数・対数関数」からの出題。前半の対数計算や対数グラフの選別は2016センター試験に、後半の対数不等式の表す領域については2007センター試験に良く似た出題でした。ここは素早く正確に片付けたい。
〔２〕は「整式の割り算（恒等式）」からの出題。誘導が丁寧です。(2)の証明部分は少し混乱するかもしれませんが、ノリで当てましょう(笑)(3)はその結果を自分で使っての計算です。
第２問
(1)を解いてる時点で…
めぐろ塾の安田センター試験っぽくて解きやすい！去年のソメイヨシノみたいに文章長くなくて良かった～
って思ってたんですが…その後のボリュームが多い、かつ問われている内容がかなり高レベル！
(2)の最初は「等積条件は、積分計算前にインテグラルを結合して、計算を楽に」ってゆ～、2023の九州大文系でも出題されている常套処理で、誘導も与えられているわけですが、その後の \(y=S(x)\) のグラフの判定で、
- \(S_1=S_2\) のとき → 極小値が０
- \(S_1>S_2\) のとき → (2)の結果を利用
と考えるところ、特に後者は思いつきづらいかもしれません。下手に時間を使うよりは当てカンで埋めて先に進めちゃった方がいいかもしれません。僕も時間内ではテキトーに埋めて片方外したんで(笑)
(3)があることを知って…
めぐろ塾の安田まだ続くんかい！
って思いました。前半は、↓のような対称性からの面積一致イメージで当てましょう。
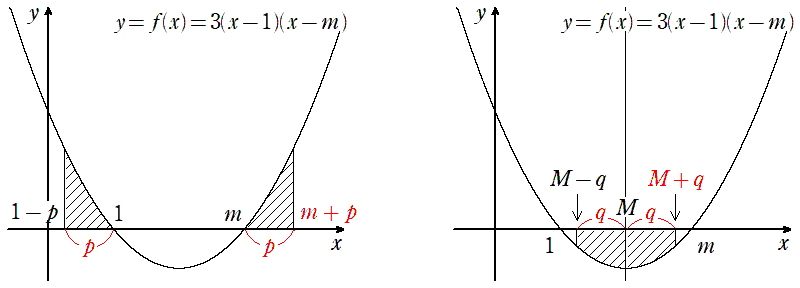
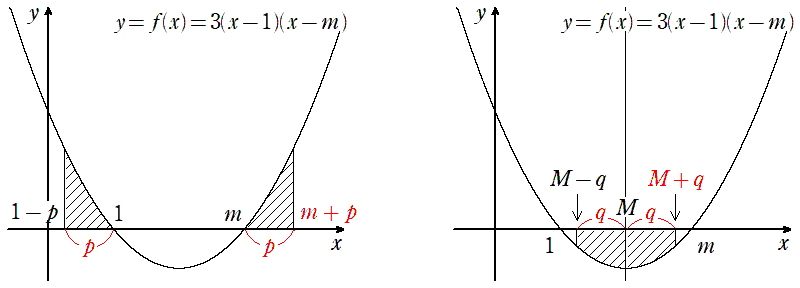
解答では最後もしっかり証明しましたが、時間内にここまで完璧に処理するのは現実的ではありません。特に理系であれば、
ど～せ \(y=S(x)\) の変曲点のこと言ってるんでしょ～
って感じでノリで選択しましょう。僕もそうしました。
第３問
2024受験者は基本的に選択してはダメな、「確率分布」の問題です。
(1)は例年に比べてかなりカンタンでした。標本から母平均に対する信頼度95％の信頼区間の計算で、その前の設問もただの公式です。流石にこの問題を選択するのであれば、
信頼度95％ → 1.96×\(\displaystyle\frac{\sigma}{\sqrt{n}}\) を標本平均から足し引き
くらいは暗記しておきましょう、添付の正規分布表から読み取るのはタイムロスです。
(2)は「確率分布」というよりは「確率」の問題で、そこそこレベルは高め。
\(E(U_5)\) で、自力で５回のうちわけを考え、確率計算
↓
問題文の「一つの直線上」と \(E(U_4)\:,\:E(U_5)\) から \(E(U_{300})\) を計算
する必要があります。因みに後者は解答のように等差数列の処理で片付けるのがカンタンです。
めぐろ塾の安田ま～でも \(E(U_4)\) は表３からカンタンに計算できますし、\(E(U_5)\) 以降を外しても－７点なんで、他で挽回すれば大丈夫でしょう。
第４問
めぐろ塾の安田全て「漸化式」からの出題で、計算も少なめでした。
(1)は、等差数列タイプの漸化式。
(2)は、特性方程式を解いて等比数列に持ち込むタイプの漸化式。
(3)は、題材になってる数列はかなり難しいです。結果論からすると、
であり、最初の方の計算はこれに気づかせるための誘導になっています。
めぐろ塾の安田でも僕も時間内ではここまで完璧に把握できず、最後の正誤を外しちゃいましたね(笑)
命題Ａのとこは帰納法証明のことを言ってるだけです。ここまで完璧に当ててれば及第点でしょう。
第５問
「空間座標」が題材で、計算量は少なくありませんが、センター試験まで遡ってのここ10年のベクトルの問題で最も解きやすかったのではないでしょうか？
めぐろ塾の安田ってかめぐろ塾↓のテキストに全部入れてるタイプの問題です。的中？(笑)
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
\(\left|\overrightarrow{\textrm{OP}}\right|\) の最小までは、\(\left|\overrightarrow{\textrm{OP}}\right|^2\) の立式が要求されているので、花子さんの式的手法でいくのが良いでしょう。
\(\left|\overrightarrow{\textrm{PQ}}\right|\) の最小は、花子さんの式的手法だと \(s\:,\:t\) の独立２変数関数の最大・最小になり、平方完成が２回必要になるのでメンドウです。解答のように、太郎さんの図形的手法でいきましょう。このとき、最初に \(\overrightarrow{\textrm{AB}}\cdot\overrightarrow{\textrm{CD}}=0\) を計算しているので、これを活用した計算ができるのがベストです。
めぐろ塾の安田一つ恨み言を言わせて頂くと…
上記のように計算すると、Ｐの座標とＱの座標は独立に計算することになります。Ｐの座標とＱの座標をセットで４点ではなく、それぞれ２点ずつにして頂きたかったです。これのせいで僕は９割を切ってしまった(笑)
総評
第２問のボリューム、難易度はかなり高かったですが、第４問「数列」の計算量が少ない、第５問「ベクトル」の出題が典型的ということで、難易度的に去年と大差はなかったと思います。
めぐろ塾の安田因みに僕も解答を打ち込む前にちゃんと時間測って解きました（もちろん選択問題は第４・５問を選択）が…
- 第２問のグラフの判定をテキトーにやって間違える… －４点
- 第４問の最後の正誤判定をノリでいって外す… －４点
- 第５問の最後の計算を見事に外す… －４点
で88点…
めぐろ塾の安田９割切っちゃってプロ講師として恥ずかしい…
でもお互いに切り替えましょう！
もう共テのことは忘れて私大に向けて勉強だっ！！
僕も解答速報で君たちと一緒に戦います(笑)
なお、本年は速報性を重視した記事にさせて頂きました。この記事を見ている高２生とかで、共テの詳しいテクニックとかを知りたい人は2023の記事↓をご参照くださいm(_ _)m
また、今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
