2024早稲田人科【数学選抜】解答速報

2024早稲田大学人間科学部の数学選抜の数学の解答速報をお届けします!
 めぐろ塾の安田
めぐろ塾の安田人員不足のため、一人で孤独にやっております(笑)
数学選抜の解答は大手予備校さんが出さないので、値的な不安は拭えません。間違えを見つけた方は、TwitterのDM等でご指摘頂けますと幸いです。既に指摘くださった方に心より御礼申し上げますm(_ _)m
【問1】(必須問題)
問題


考え方



小問集合です。
(1)は、とりあえず、
\(x^{2032}-194x^{2024}+x^{2016}\)\(\:=x^{2016}(x^8-194x^4+1)\)
とくくってみましょう。1の虚数立方根ωの問題の経験がある程度ある人であれば、
どうせ \(x^8-194x^4+1=0\) になるっぽくね?
と思えるはずです。これに、
\(x+\displaystyle\frac{1}{x}=t\) とすると、\(x^2+\displaystyle\frac{1}{x^2}=t^2-2\)
という有名処理の経験を照らし合わせれば、どんどん2乗していけば良いことが分かるでしょう。
(2)は、チョー典型問題なので絶対に外せません!ってかめぐろ塾のテキストは「1の目」、「500回」でテキストに入れてます、的中!(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
5の目が \(k\) 回でる確率 \(p_k\) を独立試行の確率として計算し、
離散変数関数なので、 \(p_k<p_{k+1}\) ⇔ \(\displaystyle\frac{p_{k+1}}{p_k}>1\) で増加範囲を調べる
だけです。「=1」が成立しちゃう場合は、最大をとる \(k\) が2つ出ちゃうんですが、こーゆ~ひっかけもありません。
(3)は、\(\sin^2●+\cos^2●=1\) でsinを計算、加法定理で \(\cos\theta=\cos\left(\alpha+\displaystyle\frac{\beta}{2}\right)\) を出して、
\[1+\tan^2\theta=\displaystyle\frac{1}{\cos^2\theta}\]
で \(\tan\theta\) を計算するだけ。記述式なので、各公式を使う際は範囲をしっかり断り、正負の判断を明記した方が良いでしょう、ルートをつけて使うので。今年のセットでは絶対に外せない問題です!



なのに僕は計算ミスしたらし~です(笑)
ご指摘頂いた方、ありがとうございましたm(_ _)m
解答




【問2】(必須問題)
問題


考え方



これは受験者の出来が悪い気がします…
結論から言えば…
\(k\) を \(x\) の式で表すと、(2次)/(1次)
↓
(分子)÷(分母)で、余りの分数の部分が整数になる条件に注目
という、整数の分数式における常套処理の問題なんですが…そこに思い至るまでが結構大変です。整数問題における3大解法、
- (整数の積)=(整数の積)の形から素因数の「拾い上げ」 → 具体値の項がないのでキツイ
- 判別式 \(D\) から範囲の「絞り込み」 → \(k<0\:,\:k>16\) となり、絞れない
- 剰余系の利用(合同式) → 有効性が見えない
を試した上で、「カンタンな文字 \(k\) について解いてみよう」って思考から解法が導かれるので。



他にも「解と係数の関係」と思った人もいるんじゃないでしょうか?めぐろ塾の生徒で受けたヤツもそう思ってしまったようですが、多分それだと解けないです。※下の追記もご参照くださいm(_ _)m
解答では、
- 分母 \(x-4\) の候補が10個あるので、全体を \(x-4\) の式として、複号同順で効率的に計算
- \(D>0\) から候補を減らす
という、思いつく限りカッコいい方法をとりましたが、こんな解答書けなくていいですよ(笑)大問1つ当たり30分使える設計なので、時間はたっぷりあります。\(x-4\) の可能性が10個であることに気づけたら、全て地道にしらみつぶして計算してください!
※追記
上のように偉そうに言ってしまいましたが、解と係数の関係でいけるようです。Twitterで優しい方が教えてくれました。ってかこっちの方がオレの解答よりキレイじゃね?(笑)受験生の方のようです、日本の未来は明るい!!了承を頂きましたので、オレの解答よりキレイな解答を掲載させて頂きます↓


解答


【問3】(必須問題)
問題


考え方



再び小問集合です。(1)はムズい。あまり見ないタイプの問題なので、個人的には解いてて楽しかったですが(笑)
- 与等式を加法定理で簡略化 → ムリ
- 正弦・余弦定理で与等式を辺の式に書き換え → 外接円の半径 \(R\) が残ってキツイ
ってとこから、
三角形の内角の和が \(\pi\) を使って \(\sin A\) を消去
↓
与等式が簡略化され、\(C\) が求まる
ってのがストーリーですが、\(A\) の値が目標なので、\(A\) を消去するのには勇気がいります。そして最後も \(\displaystyle\frac{\pi}{12}\) の三角比の形をある程度知ってないと手が止まってしまうので…受験者の出来は良くないでしょう。
※\(B\) が有名角になるので、正弦定理で \(B\) を出しちゃえば \(\displaystyle\frac{\pi}{12}\) の三角比を使わずにいけるようです。ご指摘頂いた方、ありがとうございますm(_ _)m
対して(2)はクソ簡単です。logをとったり外したりするとき、底 \(a\) と1の大小で場合分けするのは法律であり、(a)はそれを聞いてるだけ。(b)は1次不等式解くだけ。この問題は絶対外せないでしょう。



こんだけディスっといて、もし僕の解答ミスってたらクソ恥ずかしいですね(笑)
解答




【問4】(選択問題)
問題


考え方
文系生徒用の選択問題です。【問5】は明らかに理系の数Ⅲ出題なので。
(1)は2次関数の最小、(2)は4次関数の最小値を求めるだけ。ここは絶対落とせません!時間かけてもいいんで、冷静にシグマから具体化して確実に当ててください!
(3)は、最初ちまたの参考書で言う \(S_n-rS_n\) 法を使う気マンマンでここまで↓打ち込んだんですが…
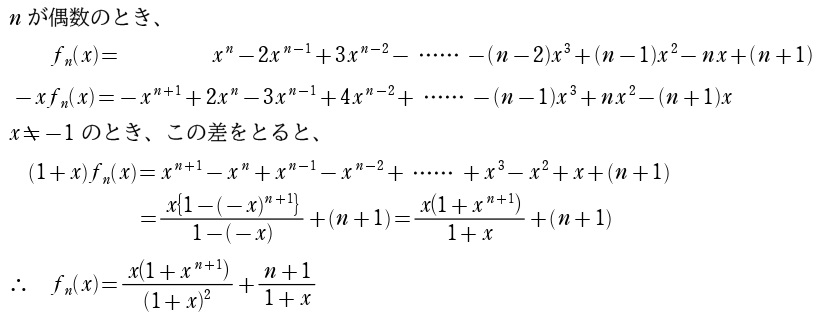
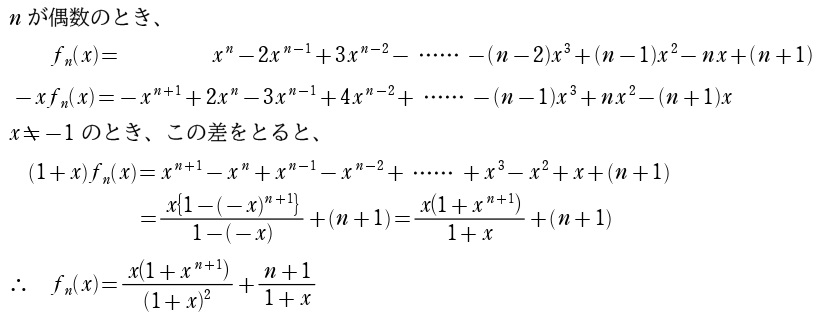



この問題って文系生徒用の出題だよな?これ、文系範囲じゃ微分できねーじゃん…
ってことで諦めるハメに(笑)同じようにしてしまった文系生徒がいたら可哀想すぎる…もし理系でこの問題を選択した人は、試してなくて申し訳ないんですが、このまま微分しちゃえば解けると思います。
文系範囲の解答となると、問題の設計からして、
(1)と(2)を実験と受け取り、答を予測
↓
帰納法で証明
でしょう。帰納法証明がかなり煩雑です。かつ、最小値 \(m\) の定義は「\(f(x)≧m\)」だけでなく、「\(f(x)=m\) となる \(x\) が存在(実際に \(f(x)\) は \(m\) をとる)」なので、解答のように、
\(f_{2l+2}(1)=l+2\) も示す
必要があります。



ここまで文系に要求するのは酷だな~
と思いました。文系生徒であれば、帰納法に気づいていることをアピールできれば及第点、\(f_{2l+2}(x)≧l+2\) まで2次関数の平方完成で言えてれば大成功でしょう。
解答




【問5】(選択問題)
問題


考え方
理系専用範囲の数Ⅲからの出題です。



おいおい…文系生徒用の【問4】より随分カンタンじゃね~かよ…理系優遇してんじゃね~よ…めぐろ塾の生徒で受けてるの文系なんですけど…
って最初見た感じは思いましたが、結果的には【問4】と同レベルの難易度でした。思考的には【問4】よりカンタンなんですが、最後の積分計算がかなりメンドくさい…部分積分を実行した後に、東大や京大が大好きな \(\displaystyle\frac{1}{\cos x}\) の積分が登場してイヤになりました。でもこの記事↓


でも書いてる通り、理系専用範囲と文理共通範囲の一番の違いは、「微積分対象関数の増加による、圧倒的な計算の複雑化」なので、その観点から言えば理にかなった出題かと思います。
因みに、最終的な値には全く自信がありません(笑)ミスを見つけた方はご指摘頂けますと幸いですm(_ _)m
解答




講評
この記事を作った後に去年2023の解説記事↓


も作成しましたが、これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 120分 | 5問 (【問4・5】は、どちらかを選択して解答。文系は【問4】を選択するしかない) | 変化なし |



に思えます。必須問題はとっつきやすい問題が増えたんですが、選択問題の難易度が上がったので。
2022と2023の合格最低点は、6割程度です。
【問1】・【問3】(2)・選択問題の前半 = 約45% の獲得は必須でしょう。合格にはこれに+αが必要です。「+【問2】がほぼできた」、「+選択問題ほぼ完答した」、「+【問3】(1)ができた」となれば合格は固いと思います。これらでなくとも、記述式なので「部分点をかき集めた」ってのでも戦えるでしょう。
でももう皆、早稲田人科の数学選抜のことは忘れてオッケー!数学選抜じゃない方式も残ってるし、他の受験校もあるはず!数学選抜じゃない方式の方が、全然問題はカンタンだから安心して!…マーク式だから部分点もらえないけど(笑)
君の受験はまだまだこれからだっ!!



僕の解答速報地獄もまだまだこれから…(笑)
君は一人じゃない!!!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








