2025北大【文系数学】解答速報

2025北海道大学の文系数学の解答速報をお届けします!
 めぐろ塾の安田
めぐろ塾の安田理系数学については↓の記事をご覧くださいm(_ _)m


1
問題


考え方



本校受験者で(1)で詰まる人はいないでしょう。
ただ微分して増減表を作るだけです。そこそこ値が複雑なんで、冷静に計算しましょう。
(2)は「\(C\) 上の点 \((-3\:,\:-6)\) を通り、」と言われているので、\((-3\:,\:-6)\) を接点と考えてはいけません。接点を \((t\:,\:f(t))\) とおき、接線を立式、\((-3\:,\:-6)\) の通過条件を処理して \(t\) についての3次方程式を導きましょう。このとき、
接点を \((-3\:,\:-6)\) としたものは明らかに答となる
↓
\(t\) の3次方程式は \(t=-3\) を重解に持つ
↓
\((t+3)^2\) で因数分解できる
ことに気づけると、解答のように一瞬で計算できるんですが…



\((t+3)^2\) で因数分解できることにまでは気づかなくていいと思います。最低限 \((t+3)\) で因数分解できることには気づきましょう。計算ミスのリスク大幅に低減できるので。
解答


2
問題


考え方
理系数学の5と式の形が似ていたんで、何か関連性があるのかと思いきや…



何も関連性ありませんでした(笑)
\((a\:,\:b\:,\:c)\) の可能性が少ないので、(1)と(2)はただ数えるだけのクソつまらない問題です…
(3)も、(2)の答が2組しかないので、余弦定理で2回計算して終了です。因みに、
(1)では、最大辺が\(c\) のときの三角形の成立条件 \(a+b>c\) を満たす組を求めている
↓
(3)で、(2)の組は(1)に含まれるので、三角形の成立条件を満たすことを断る
部分には部分点が配置されているように思えました。通常の三角形の成立条件は、↓の記事でも紹介しています。


(1)との関連性に気づけなかった場合でも、(2)の2組が通常の三角形の成立条件を満たすことは断って欲しいところです。
解答


3
問題


考え方



わ~い、面白そうな問題きた~
って喜んでたら…誘導が激しすぎてあんまり面白くありませんでした(笑)
係数が \(n\) の式の3項間漸化式だけど…
↓
(1)の階差数列の誘導で、\(a_{n+1}-a_n\) や \(a_{n+2}-a_{n+1}\) を作っとく
↓
勝手に \(a_n\) の3項間が、\(b_n\) の2項間漸化式に書き換わってしまう
ので…



後はめぐろ塾↓の…


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
漸化式のフローチャート↓
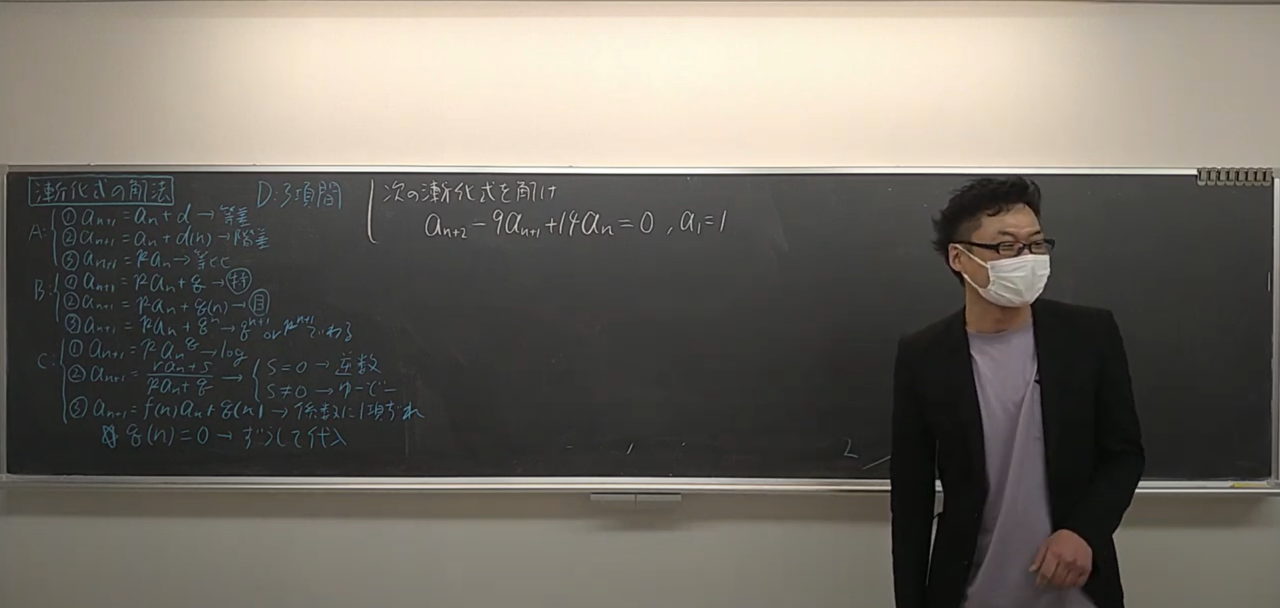
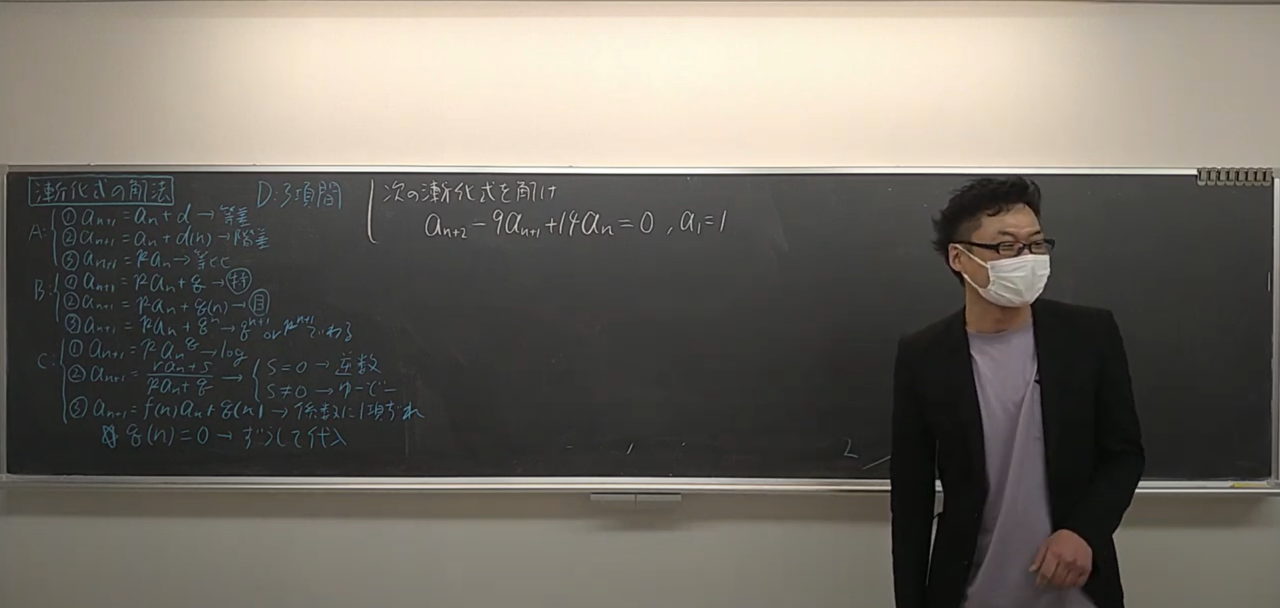
のC:③とA:②で終了。解答ではC:③部分を係数に1項ずれを作って処理していますが、☆でずらして代入していっても大丈夫。
(3)のシグマ計算も、部分分数分解するチョー有名タイプです。
全体的に完答はマストな問題。
解答


4
問題


考え方



この問題は苦しんだ受験生が多いんじゃないでしょうか?
\(f(x)\) が具体的に与えられない「抽象関数」の問題
↓
与えられた \(f(1)=2\) を使えるように、\(x\) や \(n\) に適切な値を代入するだけ
なんですが、類問の経験がないと結構キツいかと…
(4)は2回代入を考えなきゃいけないってことで、個人的には解いてて楽しかったんですが、文系生徒には厳しい気もします…
(2)や(4)は文系生徒には厳しいんですが、(1)と(3)は適切な値の代入にさえ気づければカンタンです。類問の経験があった人は、(1)と(3)は当てて欲しい問題。
解答


講評
昨年2024の解答速報も行いましたが↓


これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 90分 | 4問 | やや難化 |
です。昨年2024は全ての問題が穏やかすぎる構成でしたが、今年2025の4はそこそこ解き応えがあったので。
1・2・3をほぼ完答していれば合格最低点は間違いないテスト!
でしょう。これに4を部分的にでも拾えれば、その分だけ数学で点数稼げたと思います。



でも…終わったテストのことはそこまで気にしないでオッケー!
記事を上げるのが遅くなってしまい、執筆時3/22は既に国公立後期試験の発表も終了している頃合いです…
受験生の皆さん、1年間本当にお疲れ様でしたm(_ _)m
どんな結果であろうと、1年間の君の頑張りは輝いてるぞっ!



胸を張れっ!!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








