2025大阪公立大【文系数学】解説・解答・講評

2025大阪公立大学の文系数学の解説・解答・講評をお届けします！

理系数学については↓の記事をご覧くださいm(_ _)m

第１問

問題

考え方

数字が出る独立試行（サイコロを投げる問題が多いです）を \(n\) 回繰り返したときの積についての確率で、非常に典型的な問題です。

問１は、０が少なくとも１回出ればいいので、余事象。

問２も、余事象で \(M_n=0\:,\:1\:,\:2\) の場合を考えて引くだけ。

問３は、４の倍数でない偶数を１回、奇数を \(n-1\) 回出せばいいだけ。

解答

第２問

問題

考え方

問１は、与等式の両辺の底を２とする対数をとって整理するだけ。

問２も、\(a=\sin\theta\) として不等式を解くだけ。めぐろ塾↓では、

logの積・商形の対数方程式・不等式
↓
置き換え

ってキーワード化する内容ですが、本校受験者には釈迦に説法でしょう。鬼門って言えるのは、

\(\sin\theta=1\) となる場合 \(\theta=\displaystyle\frac{\pi}{2}\) を失念しない

とこくらいかと。

解答

第３問

問題

考え方

与式に整数の積の形が作られているので、素因数の「拾い上げ」を考えるだけ。

• 問１は、大小をつけるように素因数２を拾うこと
• 問２は、左辺の３つがすべて偶数であることに注目し、大小を素因数３でつけるように拾うこと

に注意して計算しましょう。やはりほぼ完答がマストな問題に思えます。

解答

第４問

問題

考え方

問１は、これ↓を使うだけ。

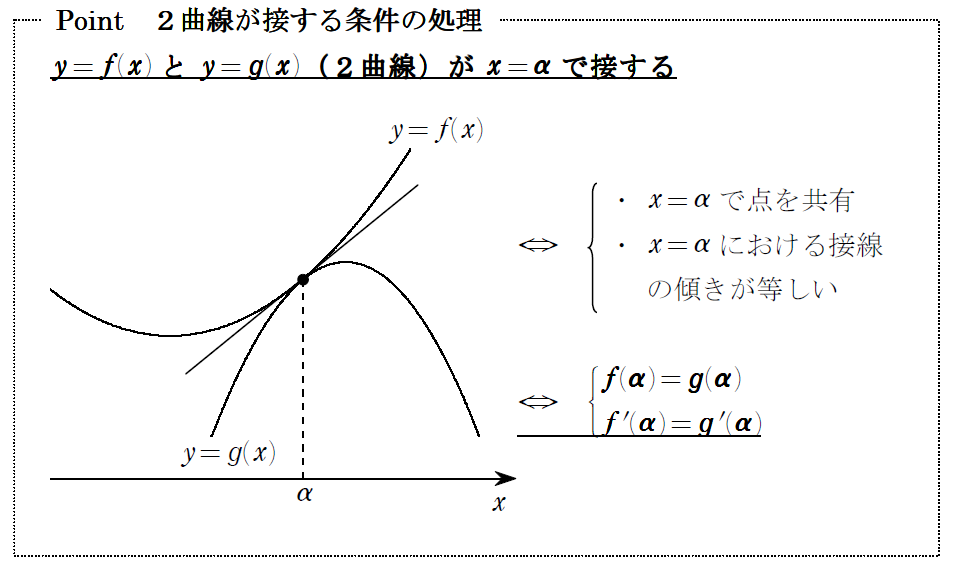
問２は、問１で

(分子の次数)≧(分母の次数)　→　(分子)÷(分母)

ってお決まりを実行してれば勝手に終了。

問３は、明らかに相加相乗平均。

問４は、面積公式（１／６公式）を使うだけ。明らかに \(C_2\) が下凸放物線なので図示は必要ありませんが、

∫(上－下)dx　→　被積分関数の因数分解　→　１／６公式を利用

という流れは記述しないと減点される可能性があるので、しっかりと記述してください。

解答

講評

昨年の解説記事↓

も作成しましたが、これと比べると…

第１問・第２問・第３問のほぼ完答が欲しいテスト！

です。これらが確保できていれば、第４問で計算ミスっちゃってても合格最低点は余裕で超えるでしょう。

今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！

君の大学受験が最高の結果になることを祈ってます！