2025東北大【理系数学】解答速報
2025東北大学の理系数学の解答速報をお届けします！
めぐろ塾の安田理系数学については↓の記事をご覧くださいm(_ _)m
１
問題
考え方
長ったらしい表現で試行が説明されていますが…
めぐろ塾の安田結局、
「＋１」の確率が \(\displaystyle\frac{3}{4}\) 、
「－２」の確率が \(\displaystyle\frac{1}{4}\)
ってだけ。
これが読み取れれば、(1)・(2)はただの「独立試行の確率」です。
(3)は(1)・(2)からして…
確率０に決まってんじゃん…
って思えるかが重要。
めぐろ塾の安田「＋１」：２個と「－２」：１個のセットが作れないと原点にもどれないので。確率０ってちょっと不安になるよね、安心して、僕も不安になった(笑)
自信を持ちましょう。これに気づけさえすれば、整数論証で示すだけです。
解答
２
問題
考え方
(1)で誘導が与えられている通りに、底を２とする対数をとれば、どの参考書にも載ってるような単純な連立漸化式が立式されるので、全体的にこれを解くだけ。
めぐろ塾の安田ちょっと気になるのは…このタイプは数列消去で３項間にして解いちゃう人も多いかなってところ。
それだと(1)の「等比数列」って部分の誘導に載れなくなります…めぐろ塾↓だとこ～いった誘導ついたときのために、数列消去よりも組み合わせて等比の解法を優先させるんですが…
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君がそ～いった授業を受けていることを祈ります。係数や公比も整数値で、計算も楽な問題です。
解答
３
問題
考え方
めぐろ塾の安田こ～ゆ～４次関数のグラフの概形変化↓をおさえていれば当たり前ですが…
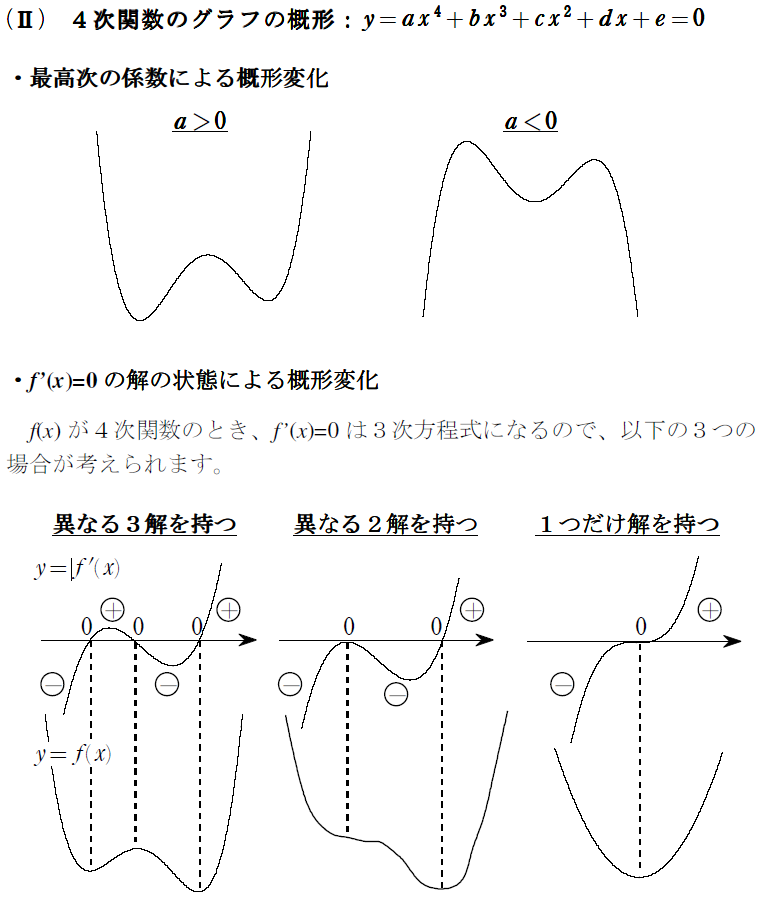
最高次の係数が正の４次関数は、極値を３つもつときしか、極大値を持ちません！
なので、３次方程式 \(f'(x)=0\) が異なる３解をもつ条件を考えて終了。３次方程式の解配置問題になりますが、因数分解できちゃうので、単純な２次方程式の解の配置で片付いちゃいます。
因みに、こ～いった極値系の問題では「符号変化」を明記するってルールがありますが、めんどくさかったので、必要「十分」条件って言葉で代用しちゃってます、悪しからずご了承ください。
めぐろ塾の安田東北大は…この解答で減点するような大学ではないかと(笑)
解答
４
問題
考え方
めぐろ塾の安田(1)は↓これ使っときましょう。
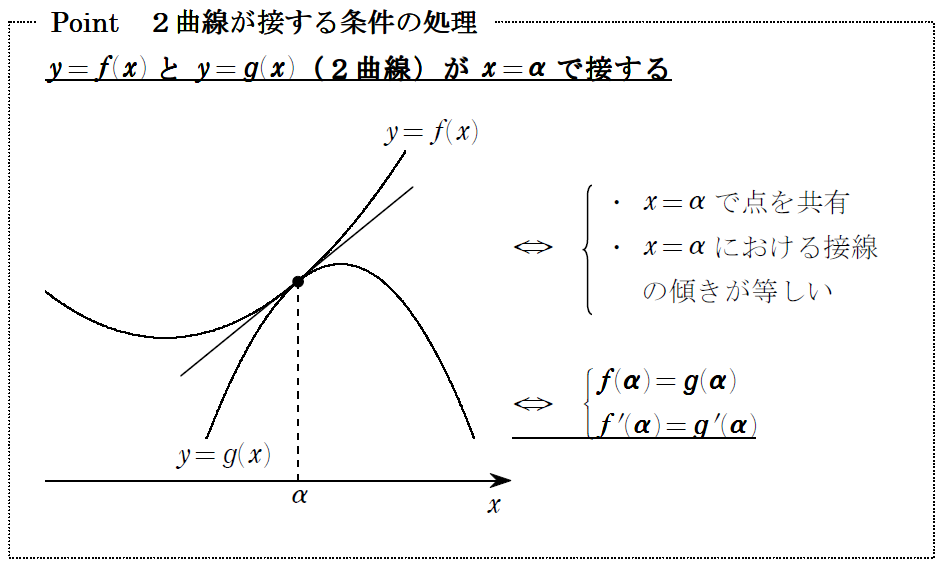
(2)は、(1)の結果から積分計算。グラフがカンタンなので、立式も楽、計算も楽です。
(3)は、(2)の結果から極限計算。(2)の最後の結果を使うよりも、整理前のを使った方が、
\(\displaystyle\lim_{x\to 0}\displaystyle\frac{e^x-1}{x}=1\) の利用
に気づきやすいかと思います。計算がカンタンすぎる、かつ結果が０になって不安になるところではありますが、自信をもって解答を書きましょう(笑)
解答
５
問題
考え方
(1)・(2)共に、空間での図形の交点なので、「直線の媒介変数表示」と「球の方程式」から冷静に計算しましょう。
鬼門となるのは(3)でしょう。この手の問題に慣れている人ほど、
平面 \(\alpha\) の法線ベクトル \((3\:,\:4\:,\:5)\) が与えられている
↓
一瞬で平面 \(\alpha\) を \(3x+4y+5\left(z-\displaystyle\frac{1}{2}\right)=0\) と立式
↓
(1)の結果の利用
めぐろ塾の安田と考えてしまうと思います。何を隠そう、僕もそうした(笑)
でもそれだと文字消去がダルいので、
(2)の結果を利用
↓
上の平面 \(\alpha\) の立式の手順を踏む
というのが正解です。(2)の結果に２乗和が登場するので、解法の軌道修正は難しくない問題でしょう。
解答
６
問題
考え方
(1)はこの記事↓とかまんまなので、詳しく知りたい人は周辺記事をご覧くださいm(_ _)m
めぐろ塾の安田(2)は正直捨て問だと思います…
- 10辺の長さが等しい十角形になるが、キレイに作図しないと気づけない。
- その十角形は正十角形でない（から円に内接しない）。ひし形が正四角形（正方形）にならないのと同様。
- 注目箇所が多く、計量に苦しむ。
- 正しく計量できても、余角・半角・積和とか使いまくり。
めぐろ塾の安田ソフトでキレイに作図できるというチート状態の僕も…
混乱とか計算ミスしまくりで１時間以上かかりました(笑)
そもそも十角形になるとこに気づけずに脱落してしまった人も多かったと思います。(1)の誘導からcos36°は計算しそうなので、この部分の部分点が拾えてれば及第点じゃないでしょうか？
解答
講評
昨年2024の解答速報も行いましたが↓
これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 150分 | ６問 | 易化 |
だと思います。サービス問題が２問だけだった去年2024に対し、１～４がサービス問題、５も大してムズくないって構成だったので。
最後だけが難しかった2023と非常に似た構成に戻りました。
１～４をどれだけしっかり完答できたかが勝負のテスト！
だったでしょう。１問程度落としちゃってても、５(1)・(2)や６(1)が拾えてれば十分に戦えると思います。
めぐろ塾の安田記事を上げるのが大分遅くなってしまい、執筆時点3/17では国公立後期試験が終了しています。
受験生の皆さん、本当に一年間お疲れ様でしたm(_ _)m
どんな結果であろうと、一年間頑張った君は素敵♪
胸を張れっ！！！
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
