2025千葉大【理系数学】解説・解答・講評

2025千葉大学の理系数学の解説・解答・講評をお届けします!
千葉大の数学の特殊性

↑でもお話ししているんですが…
千葉大の数学の入試では、
文系数学と理系数学が同じ冊子で配られる!
 めぐろ塾の安田
めぐろ塾の安田ことは、千葉大を受ける人は覚えておいてください。
かつ…
理系数学では、学部・学科によって解く大問が変わる!
ことになるので、理系の人は解く大問を間違えないように気を付けましょう!



表紙を入手できなかったんですが、多分2024と同じく↓の形かと思います。表紙お持ちの方がいらっしゃったら教えて頂けると幸いですm(_ _)m
| 学部・学科等 | 解答する問題番号 | 試験時間 |
|---|---|---|
| 教育学部(中学校コース数学科教育分野) | 3~8の6問 | 150分 |
| 理学部(物理学科、化学科、生物学科、地球科学科) 工学部 情報・データサイエンス学部 園芸学部(園芸学科、応用生命科学科、緑地環境学科) 薬学部 先進科学プログラム(物理学関連分野、工学関連分野、情報・データサイエンス関連分野) | 4~8の5問 | 120分 |
| 理学部(数学・情報数理学科) | 4~9の6問 | 180分 |
| 医学部 | 5~9の5問 | 120分 |
本記事では理系数学を対象とするので、大問4~9の解説・解答・講評となります。
教育学部(中学校コース数学科教育分野)を受験する人は、大問3については文系数学の記事をご覧ください。
4
問題


考え方
めぐろ塾の問題集の問題↓


と酷似した典型問題。



凄い難しいんですが、頻出内容です。めぐろ塾だとめっちゃ時間かけて扱います。最後の極限はカットされてるんですが、はさみうちを使うのはオマケみたいなものなので、理にかなった出題かと思います。
典型内容なので、詳細は省きます。解けない人は…
やばい…
って認識だけ持って、類問を持ってる問題集で探して演習するか、そ~ゆ~のメンドい人はめぐろ塾↓へのご入塾を検討ください(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
(1)はこの系統の問題でお決まり。帰納法を使うだけ。分子が3次になるので、ちょっと示しづらいけど頑張りましょう。
(2)はただ問題のボリュームを増やすだけの設問。差をとって、やっぱり分子が3次になりますが頑張りましょう。
(3)は…めぐろ塾では「漸化不等式」って呼んじゃってるんですが、これを立式してずらすだけ。\(a_n-3\) の評価には、当たり前に(1)を使いましょう。
一般難易度としては難しい問題なんですが、典型なので今年のセットだと完答はマストです。
解説




5
問題


考え方
ランダムウォークの問題ですが、全体的に、\(y\) 方向の「+1」と「-1」の回数を同じにするってことで、状況は把握しやすいでしょう。
(1)は \(y\) 方向の「+1」と「-1」を3回ずつ起こすだけ。(2)・(3)は、3回・2回・1回・0回ずつで場合分けです。(3)は \(y_1\:,\:\cdots\:,\:y_5\) がすべて0以上になるものを順列で数えちゃえばいいでしょう。解答のように(2)と逆に考えていくと、結果が流用できるんですが、ま~当たってれば何でもいいです(笑)



因みに…大手さんが解答だしてないので、自分の計算結果に全く自信がありません(笑)ミスを見つけた方はご指摘お願いしますm(_ _)m
すべての場合で「反復試行の確率」として計算するだけですが、計算ミスは起きやすい問題でしょう。考え方はしっかりと記述し、計算ミスしたときに部分点を確保することを意識したい問題。
解説




6
問題


考え方



(1)の計算をクリアできるかが鬼門の問題。
解答のように、
円 \(C\) の中心Bの \(y\) 座標を \(b\) と設定(図を考えれば、\(x\) 座標は \(r\))
↓
曲線 \(D\) の点Aにおける法線がこれを通過する条件から、\(b\) を \(a\:,\:r\) で表す
↓
AB=\(r\) から、\(a\:,\:r\) の等式を導く
とするのが、思考的には一番カンタンかと思います。鬼門は、最後 \(r\) を \(a\) で表すときに、
下手に展開せず、両辺に2乗を作ってルートをとる
ところで、これに気づかずに解の公式を使うと破綻しちゃうかな~って感じです。
ここさえクリアすれば、(2)は差をとると平方が出来て終了、(3)はただの求積。



因みにソフトでの作図で(1)の結果の正解は確認してるんですが、(3)の最終結果は全く自信がありません(笑)ミスを見つけた方はご指摘頂けますと幸いですm(_ _)m
解説




7
問題


考え方
(1)~(3)までで凹凸を調べたグラフの図示
↓
(4)で接線の存在問題
という極めて典型的な流れの問題ですが…



(1)と(2)の微分計算メンドくさすぎるだろぉおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおおー!!!
と、受験生の皆様の気持ちを代弁して叫ばせて頂きます…
特にテクニックも使えず、ひたすら商の微分、合成関数の微分、積の微分を繰り返すだけですが…メンドくさすぎる…
僕も(2)の最後の因数分解でミスってて、(3)のソフトでの作図中にミスに気づいた次第です…
(2)の微分計算さえクリアすれば、\(y\) 軸対称性(\(f(x)\) は偶関数)から \(x≧0\) に限定して考えるだけですが…



もっかい叫ぶ。
計算メンドくせぇええええええええええええええええええええええええええええええええええええー!!!
下手に計算確認の時間は取らず、計算ミスってるの覚悟で(4)の接線の存在を接点の \(x\) 座標の存在で考える旨まで記述し、最低限の部分点を拾うのが大事な問題かと思います。
解説






8
問題


考え方
文章長い割に、これは楽でした。
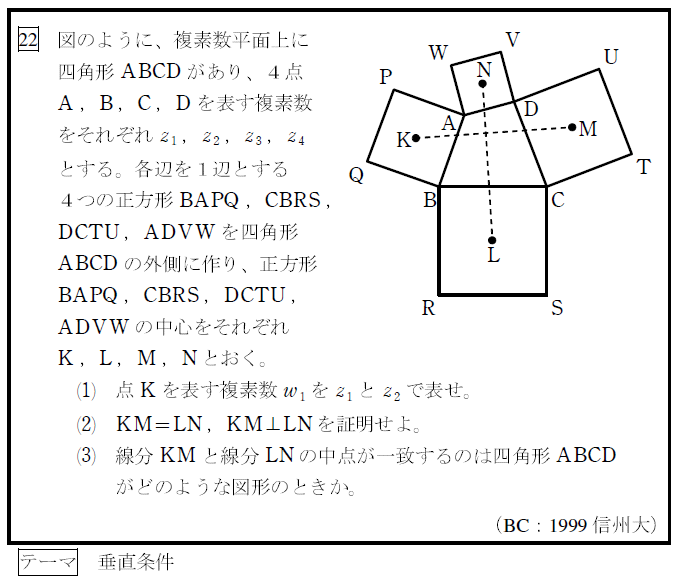




めぐろ塾の問題集のこれ↑とほぼほぼ同じ問題だったから(笑)めぐろ塾↓的中!!!今年千葉大受ける予定だった生徒、理科大受かってたから受けなかったけど(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
ま~この問題の経験なくても、「ナポレオンの定理」とかを複素数平面で証明したことのある人とかであれば困らない問題でしょう。
(1)で、複素数平面における「回転」から、中心を頂点の複素数で表す
↓
(2)で、その結果を4回使って、4中心を4頂点の複素数で表す
↓
4中心の差の複素数分数式の純虚数条件から証明
します。(2)の複素数分数式の整理では、解答のように、
証明結果から、\(i\) か \(-i\) になるに決まってる
↓
取りあえず分子を \(i\) でくくってしまう
と考えることが大切です。(3)は複素数とベクトルとの対応から、対辺のベクトルの一致を言って「平行四辺形」とします。
カンタンな問題ではありませんが、今年のセットで言うと完答はマストな問題かな~と思います。
解説




9
問題


考え方



やはり千葉大の9は難しい…
恐らく、解答のように、
- (1)・(2) → 面積評価
- (3)・(4) → 平均値の定理
で解くのが大学側の想定している解答ではないかな~と思います。色々試しましたが、(2)は面積評価じゃないとムリそうなので。
\(F\) に台形の面積公式の形が登場しているので、「面積評価」に気づきにくい問題ではありませんが…
\(f(x)>0\) が確認できない → 「面積評価」していいものか悩む



とゆ~鬼畜仕様(笑)ま~「面積評価」から得られる結果は、基本グラフが \(x\) 軸より下でも成立するので、解答では軽い言及に留めました。
ってかそもそもソフトでの作図がダルかったので、最初僕は↓で(1)を解いたんですが…


これだと(2)はムリでした…
しょうがないから「面積評価」方向で解答を打ち直しましたが、
- (2)は式的に整理してから「面積評価」を考えると、凄い論証しづらい
- 設問の式の形を信じ、接線の作る台形との「面積評価」で成功するけど、類問の経験ないとムリ
な感じです…



前の設問が証明問題ならば、解けてなくても証明結果を使って次の設問は解ける!
って数学の鉄則を守り、(1)→(3)で解くのが良いでしょう。僕も時間内だったら(1)→(3)→(4)って解いて、(2)は捨てていたと思います。
(3)は不等式に変数・関数差と微分が登場しているので、「平均値の定理」を使うことは明らかでしょう。(4)は、(3)の評価前の式に「平均値の定理」を使うって鬼門はありますが、ま~「平均値の定理」に慣れている人であれば対応できるかと。



毎年ですけど…ホント千葉大の9はムズイですね…
(1)と(3)が解けてれば及第点に思えます。
解説




講評
去年2024の解説記事も作成しましたが↓


これと比べると…
| 解答方式 | 試験時間・大問数 | 難易度 |
|---|---|---|
| 記述式 | 学部・学科によって変わる | 変化なし |
に思えます。例年通りですが…重量級の問題ばっかりで…



作図も多くて…途中で解答作るの諦めそうになりました(笑)
これ解かされる受験生の皆さん…ホントに可哀想…
典型問題である4と8を完答し、後は部分点をかき集める!
のが大事なテストだったでしょう。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!







