2023東工大【数学】解答速報

2023東京工業大学の数学の解答速報をお届けします!!!
 めぐろ塾の安田
めぐろ塾の安田試験日に家族サービスで旅行中だったんで、伊東園ホテルズにパソコン持ち込んで打ち込みました(笑)
伊東園ホテルズで数学解いた初めての人間ってオレじゃない?(笑)
ちまたでも「今年の東工大の数学は難化だ~」って騒がれてますが…



冷静に思考すれば、いつもと大して変わらない
ただ、良くもま~ここまで「見た目をムズそうに作問してきたな~」とは思います。
1
問題


考え方



問題文が1行ってゆーラスボス感(笑)
に惑わされてはいけません。
- 積分計算は不可能
- 「整数部分を求めよ」=「不等式を作れ」=「評価せよ」ってことだから、被積分関数の不等式を作ってインテグラルつけちゃうのが最有力
- \(x\) が十分に大きいとき、\(x\) は \(e^x\) に比べてカスみたいなもん
- グラフから、\(x≧0\) で \(x<e^x\)
を意識すれば、 \(0≦x<e^x\) ⇔ \(e^x≦x+e^x<2e^x\) ⇔ \(\displaystyle\frac{1}{e^x}<\displaystyle\frac{2}{x+e^x}≦\displaystyle\frac{2}{e^x}\)
これを定積分することで、 \(1-\displaystyle\frac{1}{e^{2023}}<\displaystyle\int_{0}^{2023}\displaystyle\frac{2}{x+e^x}dx≦2-\displaystyle\frac{2}{e^{2023}}\)
\(e^{2023}\) がとてつもなく大きいことを意識すれば、整数部分が1であることはすぐに分かります。



だからこの問題の本番は、1より大きいことの証明。
これには色んな方法がありますね…面積使ったりとかもできるし…
伊東園ホテルズに向かう車を運転しながら、最もキレイな解法を探してみましたが…



「これだっ!!」ってゆーべストなのは見つからなかった(笑)
解答速報によって、証明法は千差万別になると思います。
多様な解答を採点する手間を買ってでた東工大に拍手!(笑)
因みに僕はソフトで打ち込んでると作図がダルイんで、



\(1-\displaystyle\frac{1}{e^{2023}}\) なんてほぼ1みたいなもんだから、\(x<e^x\) の評価の精度をちょっとだけ上げとこ~、ってことで…





ことから \(x+1≦e^x\) ってのを証明して使いました。
このグラフの状態も大学受験では大事だよ!
\(\displaystyle\lim_{x\to0}\displaystyle\frac{e^x-1}{x}=1\) って公式とか覚えやすくなる。
でもこの方法も… \(1.8>\sqrt{3}\) とかを強引に作って使ってるし…



我ながら個人的に好みじゃない(笑)
解答


2
問題
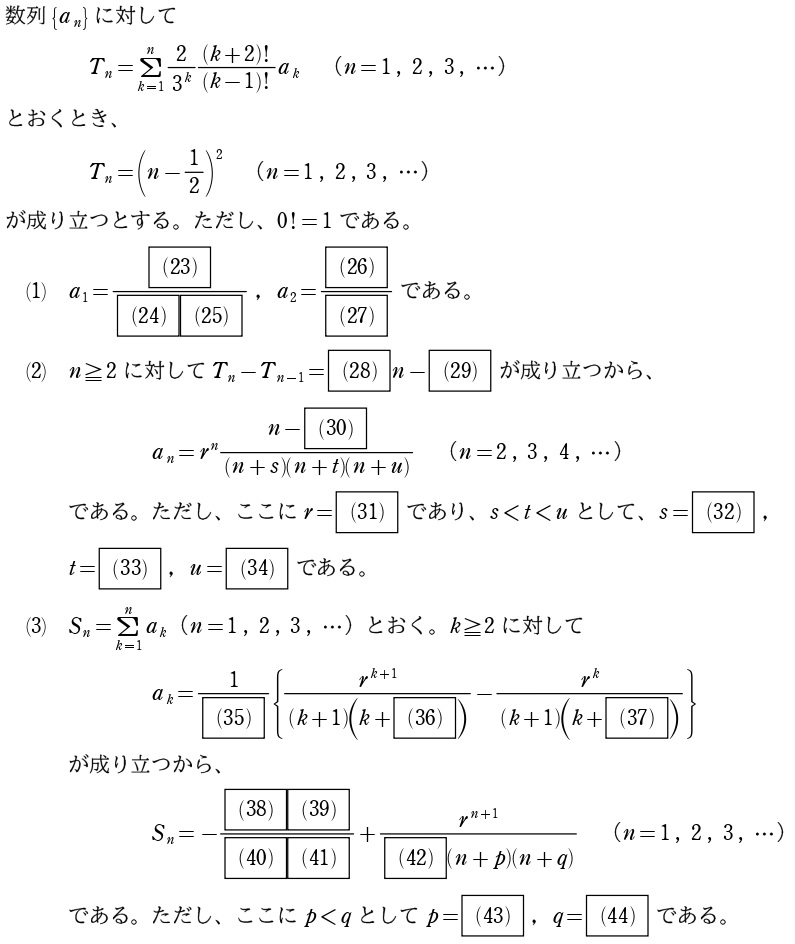

考え方



問題文の短さによるラスボス感、続く(笑)
- 未知整数確定で素因数の拾い上げを行うのは明らかなのに、因数分解が終了しちゃってる(フツーは因数分解するとこがメイン)
- 右の素因数分解で…素因数何個でてくんだよ…
- 東工大だから何かやらかしてくんじゃねーか?
ってことで、数学できる人ほどイヤに見える問題ですが(笑)
\(x^3-x=(x-1)x(x+1)\) も \(y^3-y=(y-1)y(y+1)\) も3連続整数の積だから、3!の倍数。
これに気づくのが全ての問題です。これにさえ気づければ…



後はしらみつぶすだけ。
…メンドイけど…(笑)
- \(y\) の範囲をある程度絞って、しらみつぶす可能性を減らす
- \(y\) の偶奇別に考えることで、可能性をキレイに整理する
とゆー、何ともカッコいい論証(見落としあったらゴメン)を伊東園ホテルズで打ち込ませて頂きましたが…



3時間ってゆー試験時間内でここまでの解答を作る自信はない、我ながら(笑)
論証が甘くても、答を当てることを重視して解いた方がいいでしょう。


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答




3
問題


考え方
今年の問題の中では最も簡単で計算量も少ない問題です!



でも確率と複素数が絡んでるからね。
「ムズそう」って思っちゃう気持ちは分かる(笑)
僕も最初は「ムズイのかな~」って思いましたが、



「3枚から2枚を順に選ぶ」だから、複素数の種類は \({}_3\textrm{P}_2\)=6通りしかない
ってことで簡単ってことに気づきました。
(1)は \(n\) 回の試行の過程を具体的に考える。
(2)は確率漸化式。
とゆー、\(n\) 回試行で王道の2解法を順に使わせる構成は、個人的に好印象でした。
解答






4
問題


考え方



問題の見た目がこっちのメンタル折ってくるよね~、回転が2回あるとこが特に。最初は僕も「私めにはムリそ~」って思ったけど…
\(x\) 軸を中心軸とする半径1の円柱と、\(y\) 軸を中心軸とする半径1の円柱の共通部分は、それぞれの \(z=t\) での断面を考えて重ね合わせると正方形になり、体積は \(\displaystyle\frac{16}{3}\)



って問題はクソ有名問題なので、やったことあるよね?
実はこの類問。僕もそれに気づくまでに時間かかったけど(笑)
この経験があれば、断面の場合分けも3つしかないので、東工大としては簡単な問題レベルなんですが…



最後の積分計算が地獄(笑)解答のように、
- かなり定積分の結合が可能
- 円の面積で時短できる定積分計算が2つある
ってとこを加味しても地獄(笑)



僕3回目、先輩2回目の結果がやっと一致しました。
他に解答だしてる人とも一致してるから多分大丈夫かと
時間内だと、体積の定積分での立式まで終了させ、円の面積での定積分計算を使用する姿勢を見せる、で部分点狙いが現実的に思えます。
解答











すまん、円を作図するのがダルかった(笑)
これ↓でゆるして~


5
問題


考え方



最後の問題で「空間」ってラスボス感に惑わされないことが大事(笑)
実はこの問題、今年の問題の中で「思考量」って観点から言えば一番簡単です。
(1)
空間の図形って、図形上の点 \(\textrm{X}\:(x\:,\:y\:,\:z)\) の方程式のことだから、「空間における点と直線の距離」って超有名内容を2回繰り返して距離を \(x\:,\:y\:,\:z\) で表す。後は「=」でつないで整理するだけ。
(2)
(1)からのノリで、「空間における点と直線の距離」って超有名内容を後2回やるだけ。
なんだけど…



計算量はヤバイ(笑)
解答の(Ⅰ)~(Ⅶ)の場合分け前までこなして、部分点を狙うのが現実的です。
※追記
他のとこの解答とか見ると、場合分け前までは正射影ベクトルで時短できるみたいですね。ま~でも図とかは考えず、計算でゴリ押しちゃった方がコスパはいいかと。ホントに計算ヤバイのは場合分けのとこなんで(笑)
解答









↑をPX=RXでやろうとすると2次式になって、この後の連立方程式解くのがキツイってゆー悪質なひっかけが(笑)
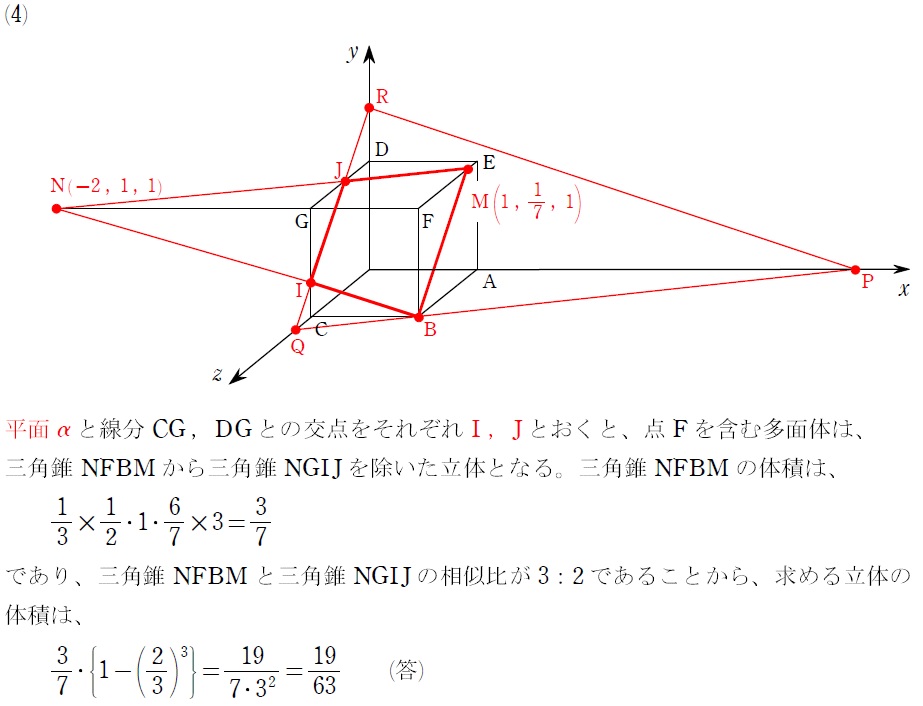



講評



東工大を一年セットで10年分以上解いてる身からすると、難易度的にいつもと大差はないんだけど…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 180分 | 5問 | やや難化 |
じゃないですかね。理由は…
- 問題の見た目のラスボス感が強すぎる
- ラスボス感が一番強い問題(問題文1行)を最初に設置しやがった
- 3と5の計算量がやばすぎる
- 全体的に場合分けが多すぎる



繰り返すけど、試験日旅行中だったんだよ(笑)
伊東園ホテルズで、ペンを使わず、解答をソフトで打ち込みながら解いてた。
冷静に俯瞰して、ペンで180分で解いた場合の自分のベストパフォーマンスを考えると、



1:完答60点 + 2:論証不備50点 + 3:完答60点 + 4:体積立式と円の面積の使用を書いた部分点狙いで40点 + 5:解答の(Ⅰ)~(Ⅶ)の場合分け前までこなした部分点狙いで40点 = 約250点/300点
だけど、「180分でも時間足りね~」ってなると思うな(笑)



ホントに調子悪かったら、こっから余裕で100点近く下がると思う(笑)
答を全て当ててる大問が2問、後は部分点を拾う記述ができてれば十分戦えるでしょう。



早慶理工の合格発表も終わったね。
私立で後期設定している大学、国立後期を受ける人は頑張って!
それ以外の受験生の皆、本当にお疲れ様!!
君の大学受験が最高の結果になることを祈ってます!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。








