2023一橋大【数学】解答速報
2023一橋大学の数学の解答速報をお届けします！！！
めぐろ塾の安田東工大を先にやってたから出遅れたけど…
大手さんまだ出してないからやっときます(笑)
１
問題
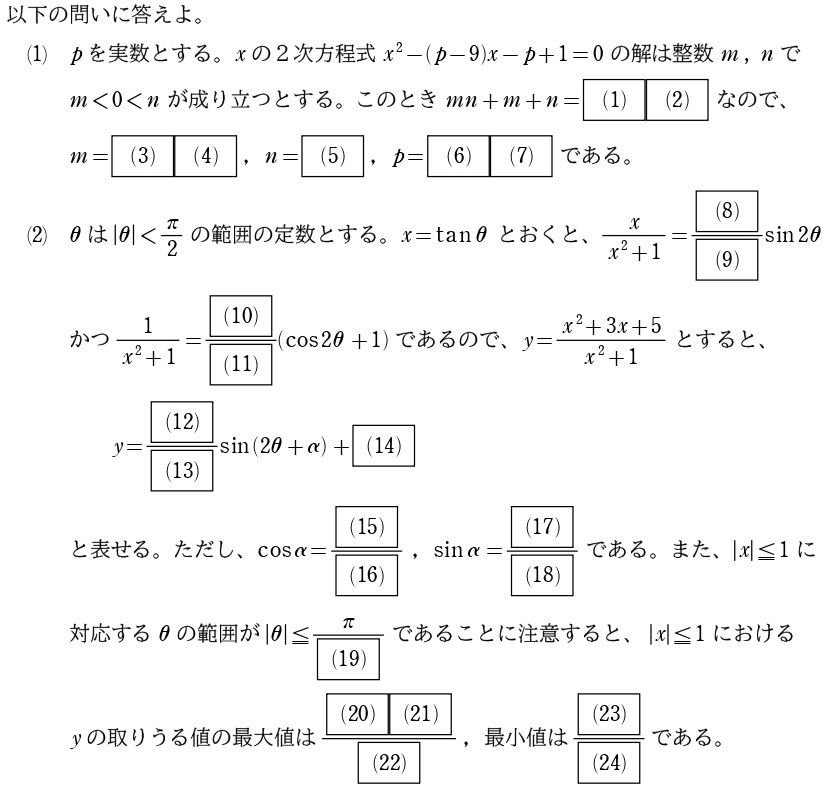
解答
２
問題
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答
めぐろ塾の安田後半とてつもなくミスってたのに気がついて戦慄した(笑)
真心こめて修正↑させて頂きました。
なぜか修正前も答は一緒だったから許して…つまるところ…
めぐろ塾の安田生きててすいませんm(_ _)m
３
問題
解答
めぐろ塾の安田ごめん、作図がダルかった(笑)
共通テストの数学ⅠＡの解説記事の第１問のとこでも言った通り、「円や球での最大・最小は中心を通るとき」ね！
因みに高さの最大値を求めるとき、Ｈを平面のベクトル方程式で表そうとすると計算が地獄になります。
めぐろ塾の安田恥ずかしながらやっちまった(笑)
その途中で平面ＯＡＢがxy平面って気づいたわ。これに気づけないで答を当てるのはほぼ不可能に思える。
４
問題
解答
めぐろ塾の安田↑が群数列として有名な問題って知ってれば瞬殺です。
式を整理するときは、解答のように \((m+n)\) をカタマリにするって意識が大切
めぐろ塾の安田(2)はムズイわ。しかも２変数２次不定方程式で問題１とネタがかぶってるじゃねーか(笑)
って偉そうに言っておいて…
めぐろ塾の安田翌日、先輩に「誘導受け取れば群数列で完結できるんじゃね～の？」って言われてベスト解答↓に気づく
作問者様、偉そうに「ネタかぶり」とかほざいて申し訳ありませんでした…
このことを考えると(1)も \(f(m\:,\:n)\) を求めずにいけると思いますが…
めぐろ塾の安田知ってる問題で試験中に冒険すべきじゃない！
ので、(1)は私めのクソ解答のままとさせて頂きます。つまるところ…
めぐろ塾の安田生きててすいませんm(_ _)m
５
問題
解答
めぐろ塾の安田クソ簡単、周期数列に慣れてる人なら５分かからないな
講評
去年は教えてるクラス内のラインでのみ解答速報をやったんですが…
めぐろ塾の安田僕は制限時間オーバーして、記述ミスとかあって95％越えくらい。
そしたら…受けた生徒がオレのミス指摘し…多分満点で…
首席で合格しやがりました！
私めの20年間 ＜ その生徒の１年間（途中から入塾だったんで、教えたの１年間）
めぐろ塾の安田で去年傷ついた僕からすると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 120分 | ５問 | やや易化 |
問題４(2)は去年のどの問題よりも難しく感じました。
でも他が簡単なんで、合格点をとる難易度的にはやや易化でしょう。
めぐろ塾の安田去年は問題１の整数で論証不備がでやすい、問題４の空間は文系には罰ゲーム、問題５の確率での連立漸化式は難易度高かったんですが…今年ムズイのは問題４(2)だけなんで。
１
\({}_n\textrm{C}_r=\displaystyle\frac{n!}{(n-r)!r!}\) を使って式を整理、\(n\) と \(k\) の２変数２次不定方程式に持ち込むだけです。
めぐろ塾の安田階乗の計算は、理系では \(\beta\) 関数とかウォリスの公式とかで使うから慣れてると思うんだけどね。文系だとそこまで経験はないでしょう。冷静に計算することが大切。
\(n\) と \(k\) のどっちで整理するかですが、僕は \(k\) の係数の方がシンプルだし、\(k\) 基準で式を見ると \((n+1)\) を複数個所に作れるってことで、あんまり迷いませんでした。
めぐろ塾の安田多分 \(n\) で整理しても大丈夫、試してないけど(笑)
\(k\) について整理した後も、解の公式を用いて、ルートの中が平方数であることに注目する、ってゆー２変数２次不定方程式の整数解を求める問題としては常套の解法を用います。
２
共通接線の存在問題なんで、接点の \(x\) 座標についての方程式の解の存在問題にする。
めぐろ塾の安田ってゆー、一橋の数学としてはサービス問題です。
解の存在問題にした後も、４次方程式が置き換えで２次方程式にできて、さらに定数分離法が使えて計算がチョー楽です。
これは絶対完答したい。
※と言いつつ、僕は後半ミスっていたようですよ…でも絶対完答したい問題であることは確実です…悔しい(笑)
３
空間で絶対値を用いたベクトル方程式があるので、
めぐろ塾の安田「どーせ球でしょ」って思ってね。ほんで四面体の体積の最大だから、中心通るときに注目
解答中にも書いた通り、鬼門は「平面ＯＡＢがxy平面であることに気づけるか」です。
めぐろ塾の安田これに気づけないで計算でゴリ押そうとすると、絶対計算ミスると思う
４
(1)は群数列の問題として極めて有名なので、この問題の経験がある人はメッチャ有利！
めぐろ塾の安田自分の問題集に５問近く入れてるんでね、個人的にはサービス問題だったんだけど…
(2)はムズイです(笑)問題１と同じ２変数２次不定方程式になるんですが、解の公式を用いた後、
- ルートの中が平方数になることに注目する
- ルートの中≧０から範囲を絞り込む
ってゆー常套手法ではできないので。これは外しちゃって良いでしょう。
※解答中に(2)のベスト解答を追記させて頂きました。特殊な２変数２次不定方程式を解かずとも、「群数列」の問題として完結できる作問だったようです。でも…僕も気づけなかったし…解けた人は少ないと思うよ…多分(笑)
５
去年の問題５の確率漸化式に比べると、クソ簡単です。
「３人でｎ回目まで」だったら場合分けが必要ですが、「３人がｎ回ずつ＝３ｎ回目まで」ってとこも簡単。
めぐろ塾の安田僕の解答を見て、「\(3k+1\:,\:3k+2\) にしないの？」って思う人は周期数列苦手だろうね(笑)
長くなるんで詳しくは説明しませんが、３つずつのグループ番号と項番号を自然数で漏れなく対応させるためには、余りをマイナス方向で設定しておくのが好ましいです。
めぐろ塾の安田これが作業化されてる人は、解答中でも言った通り、ホントこの問題は５分かからない。
総評
問題１・２・５を完答して６割確保してれば大丈夫！
でしょう。
めぐろ塾の安田問題３で平面ＯＡＢ＝xy平面って気づけなくても部分点はもらえるし、問題４(1)を知ってたら８割越えだっ！！
２完できなかったぁああああああああああああああああああー！！！
って人も希望は捨てないで！
めぐろ塾の安田社会学部みたいに数学配点低いとこなら、それでもワンチャンある！部分点拾ってれば！！
いずれにしても…
君の大学受験が最高の結果になることを祈ってます！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
