2023京大【理系数学】解答速報

2023京都大学の理系数学の解答速報をお届けします!
「解答遅報」になっちゃいましたね(笑)
でもプロ講師は毎年の京大の理系数学は解かないといけないってゆ~法律があるので(笑)



どーせ解くから、私めの解答はこのブログにさらさせて頂きます!
他の「解答速報」さんで答あわせできる安心感バンザイ!!(笑)
1
問題


考え方



最近の京大に多い、小問集合です。
問1
部分積分するだけ。最初に \(\log(x^2)=2\log x\) ってするとちょびっとだけ計算は楽になりますが、やらない方がいいかと。



厳密には \(\log(x^2)=2\log|x|\) なんで。ま~減点はされないと思うけど(笑)
問2
2021早稲田理工の数学の[Ⅱ]とほぼ同じ問題です。



早稲田理工を併願して、過去問対策してた人が有利だね
\(x^5-1=(x-1)(x^4+x^3+x^2+x+1)\) を作り出すことを考え、整数問題よろしく二項定理を用います。



2021早稲田理工で出題されたときは「目新しい!」って思ったんだけど…これ経験してるとパクリに見えちゃう(笑)
解答


2
問題




- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
考え方
「4点O、A、B、Cが同一平面上にない」=「1次独立」ってことなんで、取りあえず \(\overrightarrow{\textrm{OA}}=\overrightarrow{a}\:,\:\overrightarrow{\textrm{OB}}=\overrightarrow{b}\:,\:\overrightarrow{\textrm{OC}}=\overrightarrow{c}\) っておいときましょう。



2直線の交点の問題なんで、後は「未知数で交点の位置ベクトルを2通りで表す」→「\(\overrightarrow{a}\:,\:\overrightarrow{b}\:,\:\overrightarrow{c}\) の係数を比較」ってゆー常套処理。
因みに、直線のベクトル方程式は未知数1つで表せるので、2直線で未知数2つ。空間で係数比較を実行すると3等式が立つので、
未知数2つ < 等式3本
↓
解を持つのが奇跡的
↓
空間で2直線はなかなか交わらない(ねじれの位置にある)



ってことで出題はそこまで多くない、作問しづらいんで(笑)
今回の問題は、\(\overrightarrow{\textrm{OR}}\) を表すのにもう1文字使わせることで、3文字3等式の状態を実現しています。



この作問は個人的には好印象。ちゃんとその部分わかってるよ~ってのを伝えるために解答中は「~を全て満たす \(k\:,\:l\) が存在する」って断ったけど…
試験中に点数にならなそ~なことにこだわってはダメ!!!



答を正確に当てて!偉そ~にコメントしといて、僕はこの簡単な計算ミスったよ(笑)
解答


3
問題


考え方
- サイコロの目の積が〇の倍数 → 余事象の利用
- サイコロの目の和が〇の倍数 → 数え上げる
くらいは公式化されていた方がいいですね。



後者は特に医学部で良く目にします。
今回は前者なんで、余事象を利用するだけです。(2)は複合事象の余事象になるので、
ド・モルガンの法則
バーは分割すると、「または」と「かつ」が逆になる
\(\overline{\textrm{A}\cup\textrm{B}}=\overline{\textrm{A}}\cap\overline{\textrm{B}}\) 、 \(\overline{\textrm{A}\cap\textrm{B}}=\overline{\textrm{A}}\cup\overline{\textrm{B}}\)
を利用しましょう。



計算もほぼありません。これで \(\textrm{P}(\overline{\textrm{A}})\) の確率書き間違えたオレって流石にヤバイと思った、我ながら(笑)
解答


4
問題


考え方



最大値も問われているので、流石に「相加相乗平均」使って終わりってほど簡単じゃない。京大だし(笑)
でも「相加相乗」を使える形ってのは気づいていた方がいいですね、すぐに分母の置き換えに気づけるでしょう。



ほんで、分母の変域さぐるのも \(x^2=t\) って置き換える
ってゆー「置き換え」を重視した作問です。
因みに単調な場合は増減表を省くのが普通なんで、一切増減表描かずに完結できます。
解答


5
問題


考え方
2016東大の理系数学の第6問と同じ系統の問題です。
〇軸上の点と、△▢平面上の点を結ぶ線分の通過領域の体積
↓
後者を△軸上にした〇△平面上での通過領域の、〇軸回転体の体積
と考えます。



因みに2016の東大は「〇軸上の点を通って、△▢平面を端とする長さ2の線分」だったので、〇△平面上での通過領域が「コンコイド曲線」って私めには意味不明の曲線になりました(笑)なので私めはベクトル方程式で強引に立体式を作成して解かせて頂きましたが
今回は棒倒しの「アステロイド」に似た曲線がでるのは、早慶理工以上の問題の経験が多い人であればすぐに分かるでしょう。
xy平面上での線分の通過領域を求める際は、
- 順像法(予選決勝法) → \(a\) の関数 \(y=f(a)\) の \(0<a≦1\) での最大・最小を求める
- 逆像法 → \(a\) の方程式 \(y=f(a)\) が \(0<a≦1\) に実数解を持つ
のどちらでやっても大丈夫です。



片方 \(x\) 軸上で最小値0は明らかだから、最大値だけでいいってことで、解答では順像法でやってます。
逆像法でやる場合も、「アステロイド」っぽいって意識しましょう。「包絡線求めとけば大丈夫でしょ~」って感じで判別式条件だけに注目すれば、答は当たります。
解答
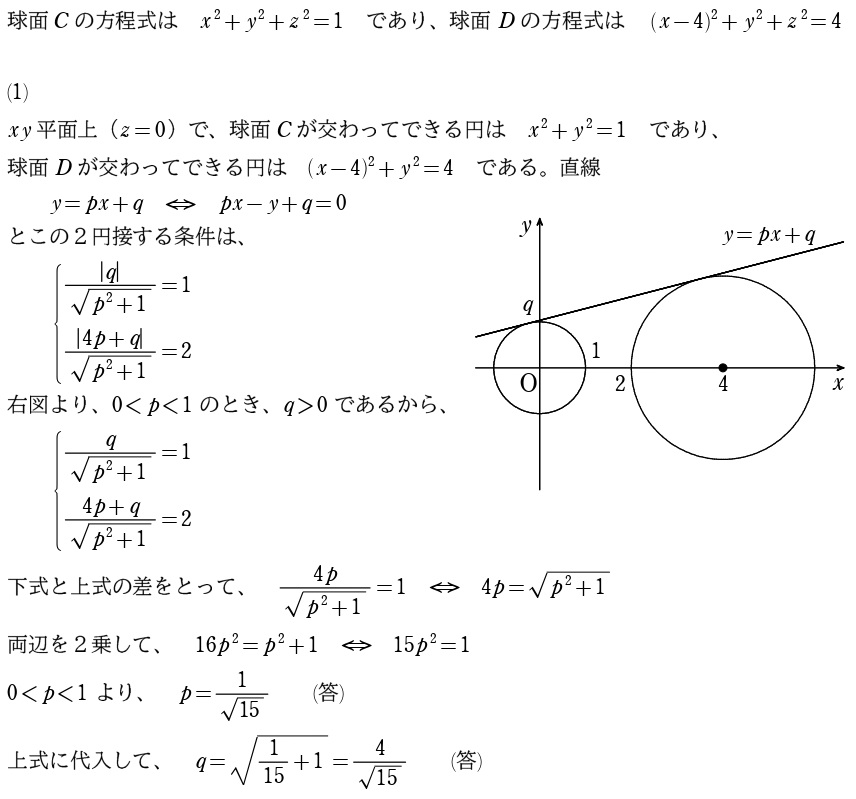



6
問題


考え方
(1)は、この記事↓


で紹介してる3倍角の公式書いときゃ大丈夫でしょう(笑)後者は2倍角2回使うだけ。



でも、オレが最も得意とする「複素数」を出題してくれなかった京大への恨みを込めて、上の記事でも紹介してる「複素数」範囲の解答を書いてやった(笑)
君たちは試験中でこんなことしちゃダメだよ!(笑)



(2)は上の記事で紹介してる「チェビシェフ多項式」への深い理解がいる。
チェビシェフ多項式
\(n\) を自然数とすると、
\(\cos n\theta\) は \(\cos\theta\) の \(n\) 次多項式で表せる
また、
\(\sin n\theta\) は \(\sin\theta\times\:\)(\(\cos\theta\) の \(n-1\) 次多項式) で表せる
今回はこれに「係数が整数」ってとこまで入ります。



(1)を誘導として捉えて、最高次の係数が \(2^{n-1}\) になってることに気づくと…
\(\cos\theta=\displaystyle\frac{1}{p}\)(\(p\) は3以上の素数)が存在すると、
\((\)\(\:p\cos\theta\:\)\(-1)(\)〇\(\cos^{n-1}\theta\)\(\:+\:\cdots\cdots\:+\:\)△\(\cos\theta+\:\)▢\()=0\)
↓
展開したとき、最高次の係数は \(2^{n-1}\) にならない
って感じで整数 \(m\:,\:n\) が存在しないことが分かるんですが…



最初こんな感じで解答作っちゃって…「ちょっとキモイな」って思って大手さんの解答見たら…この部分整数論としてキレイに証明できるんですね…後発特権でカンニングさせて頂きました!(笑)
他にも、
- チェビシェフ多項式の帰納法証明で、3項間漸化式のシステムに基づく証明が必要
- その際、\(\cos(k+2)\theta+\cos k\theta\) に和積公式を使って \(\cos(k+1)\theta\) を作る
とゆー、チェビシェフ多項式の証明の経験がないとほぼムリな問題なので、受験者の出来は良くないと思います。
解答
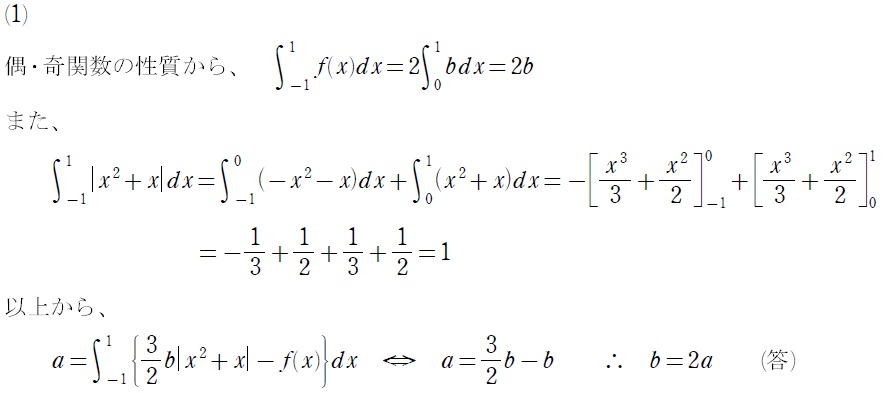




講評
ちまたで「2023の京大理系数学がとんでもなく易化」って言われてたから、東大より先にやりましたが…



そこまで簡単じゃねーじゃね~か、だまされたよ(笑)
でも去年と比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 150分 | 6問 | やや易化 |
ですね。満点をとるのは厳しいけど、1~4の難易度が低すぎる・計算量が少なすぎるので、合格最低点は上がるかと。



僕みたいに2や3でミスると厳しくなる(笑)
1~4をどれだけミスなくとれたかの勝負になるでしょう。



執筆時が国立前期の発表周辺なんだけど…後期受ける人は切り替えて頑張ろう!いずれにしても…
君の大学受験が最高の結果になることを祈ってます!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。








