2024同志社大全学部【理系数学】解答速報

2024同志社大学の全学部日程の理系数学の解答速報をお届けします!
 めぐろ塾の安田
めぐろ塾の安田人員不足のため、一人で孤独にやりました(笑)
Twitterでミスを指摘してくださった方、補足があったことを教えてくれた受験生の方に心より御礼申し上げますm(_ _)m
[Ⅰ]
問題
![[Ⅰ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]問題-1.jpg)
![[Ⅰ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]問題-1.jpg)
考え方
小問集合です。昨年↓


と同じく、(1)が「n回試行の確率」、(2)が「複素数平面」からの出題でした。
(1)
「n回試行の確率」の<方針1>「n回の過程を具体的に考える」、<方針2>「確率漸化式」のうち、<方針1>「n回の過程を具体的に考える」です。計算量も多くなく、カンタンです。



なのに私めはほぼ全滅させて頂きました(笑)
このブログを早めに見た受験生の方々を不安にさせてしまったかもしれません…君の答が正解です!私めがバカすぎただけm(_ _)m
速報当日の昼間に他の予備校の依頼で東海大医学部2日目の解答速報打ってたんですけど…大問2つが両方とも漸化式で…1つが確率の連立漸化式たてる問題だったので…



またかよ…って思って<方針2>「確率漸化式」で解いたら結構複雑で計算ミスしまくりました(笑)
Twitterでミスを指摘してくださった方、本当にありがとうございますm(_ _)m
受験生のみんな、前日にやった解法とかに引きずられないように!僕みたいに大人になって恥をかきたくなかったら(笑)
ミスをなかったことにするのはフェアじゃないので(笑)Twitterで教えてくださった方の<方針1>「n回の過程を具体的に考える」を本解答に、僕の<方針2>「確率漸化式」は別解で載せておきました。現在2024年2月時点で高2の人、別解はあまり参考にしないでください(笑)
(2)
「複素数平面」の軌跡としては典型的な形であり、
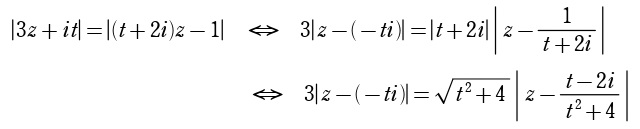
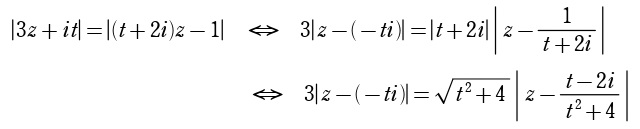
として「点 \(-ti\) と \(\displaystyle\frac{t-2i}{t^2+4}\) を結ぶ線分を \(\sqrt{t^2+4}\):\(3\) に内外分する点を直径の両端とする円」と求める、「アポロニウスの円」を用いた解法と、解答に掲載している「両辺を2乗して、円の方程式の一般形 \(az\overline{z}+\overline{\beta}z+\beta\overline{z}+c=0\) の形に持ち込む」という2つの解法があり、通常は前者の方が楽です。



ただこの問題は比も点も複雑なので、後者じゃないとキツい…
小問集合としては重い出題ですが、去年の問題と比べればマシでしょう。
因みに、記述式としても恥ずかしくないレベルの解答を打ち込みましたが、複素数平面における円の方程式の一般形の変形に慣れている人であれば、解答4行目の式、
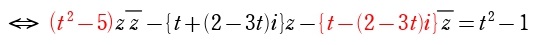
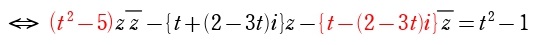
の時点で、中心を表す複素数 \(w=\displaystyle\frac{t-(2-3t)i}{t^2-5}\) が読み取れます。マーク式(答のみ解答)なので、円の方程式全体の変形は考えずに解いてしまった方が良いでしょう。



って偉そうにコメントしといて、ここでも1つ計算ミスしました…
(1)のミスを指摘してくださったTwitterの方がここも指摘してくださった…重ねて御礼申し上げますm(_ _)m
解答
![[Ⅰ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答①-4.jpg)
![[Ⅰ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答①-4.jpg)
![[Ⅰ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答②-2.jpg)
![[Ⅰ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答②-2.jpg)
![[Ⅰ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答③-5.jpg)
![[Ⅰ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答③-5.jpg)
![[Ⅰ]解答④](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答④.jpg)
![[Ⅰ]解答④](https://www.megurojyuku.com/wp-content/uploads/[Ⅰ]解答④.jpg)
[Ⅱ]
問題
![[Ⅱ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅱ]問題-1.jpg)
![[Ⅱ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅱ]問題-1.jpg)
考え方
典型的な「ベクトルの1次結合」からの面積比の問題で…



今年のセットの中で異様にカンタンでした。合格点をとるためには、この完答はマストに思えます。
(1)・(2)は、表したい点まわりの線分比が分かるので「1次結合<解法1>」。
(3)は、表したい点Pが交点なので「1次結合<解法2>」。因みに解答のように、2直線の方向ベクトル \(\overrightarrow{\textrm{OC}}\:,\:\overrightarrow{\textrm{MD}}\) をそれぞれ4倍、\(1+x\) 倍して係数を整数にして用いると、その後の連立方程式を解くのがクソ簡単になります。
- 係数に文字 \(x\) が含まれる
- 問題文で文字が使われすぎてて、(3)で設定する2文字をどれにするか迷っちゃう
とかイライラする部分はありますが、冷静に完答してください。



これは誰かに値を確認してもらっていませんが、流石に間違えてないと思います(笑)(4)で三角形OMBの成立条件 \(2<x<4\) を満たす答が出ているので。
解答
![[Ⅱ]解答](https://www.megurojyuku.com/wp-content/uploads/[Ⅱ]解答.jpg)
![[Ⅱ]解答](https://www.megurojyuku.com/wp-content/uploads/[Ⅱ]解答.jpg)
[Ⅲ]
問題
![[Ⅲ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]問題-1.jpg)
![[Ⅲ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]問題-1.jpg)
考え方
(1)~(3)はひたすら計算するだけです。



計算ミスに注意!
(2)で「放物線の2接線の交点の \(x\) 座標=2接点の \(x\) 座標の平均」とか知ってる人は結果に安心できるでしょう。
(3)でヘッセの公式からOHを求めると、
\(p\) の値に関わらず、OH=\(\sqrt{2}\)
↓
点Hの軌跡は、Oを中心とする半径 \(\sqrt{2}\) の円周上
と分かるところまではカンタンなんですが…ここから鬼門が(笑)
鬼門の1つ目、(4)で点Hが円のどの範囲を動くかを判断するところ。(3)まででスゲー傾きを求めさせているので、解答では \(p\) の範囲を傾きの範囲に変換してやりましたが、傾きが存在しない(\(y\) 軸平行の)場合に言及するのとかかなりダルかったです(笑)
鬼門の2つ目、(5)の線分の通過領域を図形的に読み取るところ。この手の問題に慣れている人ほど、


↑の記事で紹介してるような式的手法(逆像法)を使いたくなるところですが、
- 端点Mが放物線 \(C\) 上であること
- (4)までの誘導
からガマンしないといけません。
鬼門の3つ目、求積計算がダルいところ。解答のように色つけた3領域で計算するのがベストだと思いますが、試験中にフリーハンドでこんなにキレイに作図できるわけはないので、計算領域を判断するのがかなり大変、かつ計算量も多いです。
因みに解答では緑色の領域の計算を、代入計算を簡略化するために \((x-4)\) 基準(代入して0になるカタマリ)で定積分する、という数学Ⅱ範囲の求積でのお決まり手法をとっています。
このおっさん何してんの?
って思った高2生とかいたら、めぐろ塾↓への入塾を検討した方がいいかもしれない…私めがこれ以上なくクドく説明して差し上げるっ!(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
と…宣伝はこれくらいにして(笑)
100分という試験時間で最後の計算まで当てるのは厳しいでしょう。
端っこの \(p=-\displaystyle\frac{1}{3}\:,\:\displaystyle\frac{1}{3}\) のときOHの傾きが \(1\:,\:-1\) になるから、なんかこの間じゃね?
的なノリで(4)まで解ければ及第点です。(5)の軌跡を図示できたらサイコーですね、その場合は取りあえず面積は立式し、計算は諦めても部分点は拾った方が良いでしょう。



因みにこの問題は先輩も解いたらしく、答が一致してたんで、最後の値も多分あってると思います。
解答
![[Ⅲ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答①-2.jpg)
![[Ⅲ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答①-2.jpg)
![[Ⅲ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答②-3-1280x923.jpg)
![[Ⅲ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答②-3-1280x923.jpg)
![[Ⅲ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答③-1-1280x1239.jpg)
![[Ⅲ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答③-1-1280x1239.jpg)
![[Ⅲ]解答④](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答④-2.jpg)
![[Ⅲ]解答④](https://www.megurojyuku.com/wp-content/uploads/[Ⅲ]解答④-2.jpg)
[Ⅳ]
問題
![[Ⅳ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]問題-1.jpg)
![[Ⅳ]問題](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]問題-1.jpg)



実際は(3)の冒頭文章が「自然数mに対して、」でした。速報中に解答でディスったら、それを見た受験生の方がTwitterで「試験中にm≧2という修正が入りました!」というとてつもなく貴重な情報をくださりましたので、それに則って問題文を変更させて頂いております。心より御礼申し上げます。残りの受験も頑張ってくださいっ!!
考え方
去年の[Ⅳ]と一緒で…出題者側が最後まで解かせる気ないですね(笑)
(1)は、「\(\sin(整数)\pi=0\)」って唱えれば終了。
(2)の最初は部分積分を2回使うだけ。\(\displaystyle\int_{1}^{m^3}f(x)dx\) はそれを使えるように置換積分するだけです。冷静に計算してください、僕は1回ミスりました(笑)(4)の時点で気づいて直しましたが。
(3)は「用いてよい」って言われてる不等式にインテグラルをくっつけて、シグマをくっつけるだけで典型です。



とここまではカンタンなんですが…(4)からが地獄(笑)
ノリで(3)の不等式に(2)の結果は代入できるでしょう。ここで、
- \(\cos(m\pi)=(-1)^m\)
- \(m\) は結構大きいから、\(m^2\) に比べて \(m\) はカスみたいなもん
- \(S_n<0\) って言われてる
って意識を持つと、\(m\) の偶奇で場合分ければ、\(S_{m^3}\) の正負判断にこの不等式が使えることが分かります。



しかしま~、両辺の \(m\) の2次式が複雑(笑)解答では、
平方完成して増減を示唆
↓
\(10≦m≦30\) での最大・最小値で評価、そのとき平方完成の式は複雑すぎるので使わない
↓
問題文で \(3<\pi<4\) って言われるから、義務感でそれを使う
ってしましたが、打ち込んでてメンドくさくてイヤになりました。ストーリーは合ってると思うんで、この部分計算ミスっててももう直さないっす、悪しからず(笑)ってか0にそこまで近くないんで、もっとざっくりとした評価でもいいかもしれない。
そして(5)の文章の意味不明さ(笑)僕は \(y=S(n)\) のグラフと \(n\) 軸の交点のイメージを持って理解しましたが、離散変数でこの意識を要求するのは受験生には酷かと。



ってか僕にも酷でした、しかもプロ講師だから \(S_n\) の単調性も断らなければいけないってゆ~法律もあるし(笑)
100分という試験時間内で完璧な解答を書くのは現実的ではないです。(3)までできれば及第点。(4)や(5)のストーリーが読めた場合は、計算で確証を得ないでも結論を書いて部分点を拾った方が良いでしょう。
解答
![[Ⅳ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答①-6.jpg)
![[Ⅳ]解答①](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答①-6.jpg)
![[Ⅳ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答②-5.jpg)
![[Ⅳ]解答②](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答②-5.jpg)
![[Ⅳ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答③-3.jpg)
![[Ⅳ]解答③](https://www.megurojyuku.com/wp-content/uploads/[Ⅳ]解答③-3.jpg)
講評
去年の解説記事も作りましたが…去年と比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| [Ⅰ]は答のみ解答、 [Ⅱ]~[Ⅳ]は記述式 | 100分 | 4問 | やや易化 |



に思えます、小問で半分しか取れなかった分際で申し上げるのも難ですが(笑)
一般目線で言えば小問集合[Ⅰ]は去年より簡単です、私めには難しかったですが(笑)
[Ⅱ]が点取り問題って意味合いで言うと去年の[Ⅲ]と対応しますが、文章の意味不明さとか空間でなく平面ってことから、去年の[Ⅲ]より簡単です。
[Ⅲ]が計算キツイって意味で去年の[Ⅱ]と対応、[Ⅳ]が最後まで解かせる気がないって意味で去年の[Ⅳ]と対応し、難易度差は感じません。
ま~それでも100分って時間だと厳しい試験ってのは変わらないです。
昨年は、合格者平均が5割をきってる学部・学科がほとんど
↓
今年は、合格者平均は5割超えるんじゃん?
って感じかと思います。



でも受験生のみんな!全学部のことはもう忘れよう!!
私立医学部の入試はそろそろ終盤だけど、一般の学部の試験はまだ始まったばかり!同志社も全学部より学部個別の方が空気読んだ出題だよ!!(笑)
君の受験はまだまだこれからだっ!!!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








