cos36°を暗記で終わらせないで!

前回の記事
.jpg)
で、「cos36°は良い子(4・1・5)」で、何も考えずにマーク式の問題を当てちゃおう!
とゆー、何とも小手先なテクニックを紹介しましたが…
 めぐろ塾の安田
めぐろ塾の安田それで完勝できるほど大学受験数学は甘くない!
作問ミスも起きない、優秀な受験生は絶対解ける。
皆がハッピーな出題です(笑)
僕は人生で100問以上解いて、20問以上打ち込んでる(笑)
理系で優秀な受験生であれば、10問程度は経験して受験するでしょう。
これが黄金比とcos36°との、大学受験数学での正しい付き合い方です。



今回の記事ではSTEP1とSTEP2にフォーカスするね!
記述式でも頻出なんだよ…
最近の有名大での記述式の出題だと…
2020中央大商第Ⅱ問





中央大って商学部でもいろいろあるんだよね(笑)東進の過去問データベースによると、「商学部(会計、商業・貿易)」らしいです
(3)で「cos36°の値」が問われていますが、記述式なので「良い子(4・1・5)」で当てても…論証しないとねぇ…(笑)



値当ててれば、暗記してるって意味で数点くれるかもしれませんが、この問題を完璧に解けないようだと…落ちるでしょ(笑)
実はこの問題の解説って、既にこれまでの記事でやっちゃってるに等しいんですよ。


の『正五角形』の図の赤の二等辺三角形を…


というように青の三角形の中に移動させて、正五角形を登場させないようにしただけ、正五角形の対角線 \(l\) を1に変えて。
因みに、上の図の青から赤を除いた二等辺三角形は、前回の記事冒頭の二等辺三角形と合同なので、この二等辺を半分に割った直角三角形からcos36°を考えるのは明らかです。
解答



いらね~と思うけど、一応この問題の解答作っとく?(笑)
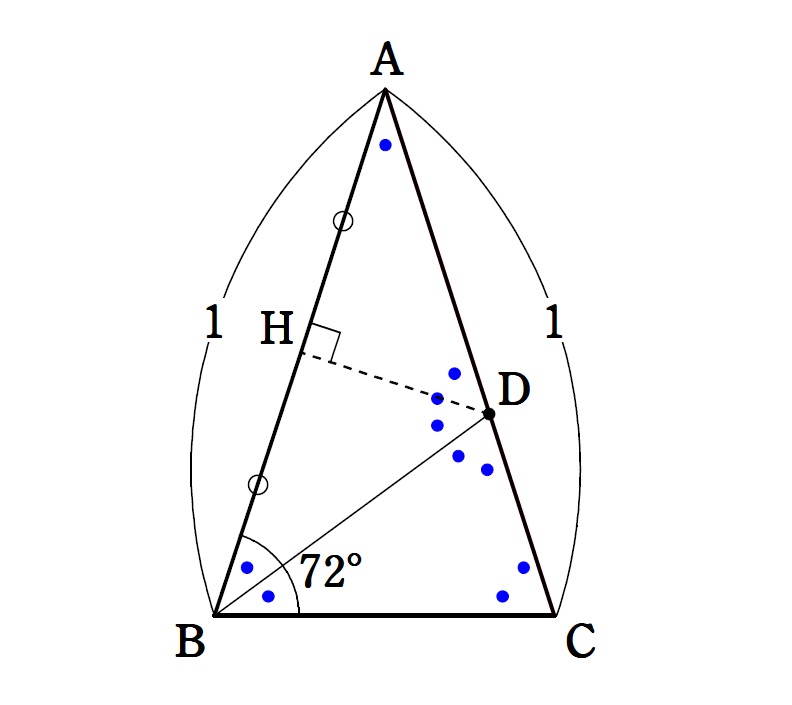

(1)
△\(\textrm{BCD}\) に注目して、
\(∠\textrm{BDC}=180^\circ-∠\textrm{BCD}-∠\textrm{CBD}\:\)\(=180^\circ-∠\textrm{ABC}-\displaystyle\frac{∠\textrm{ABC}}{2}\:\)\(=72^\circ\) (答)
(2)
(1)より、
\(∠\textrm{BDC}=∠\textrm{BCD}\)
よって \(△\textrm{BCD}\) は二等辺三角形であり、\(\textrm{BC}=x\) とすると、
\(\textrm{BD}=\textrm{BC}=x\)
ここで \(△\textrm{ABC}\) に注目すると、
\(∠\textrm{BAC}=180^\circ-2∠\textrm{ABC}\:\)\(=36^\circ\:\)\(=∠\textrm{ABD}\)
よって \(△\textrm{DAB}\) は二等辺三角形であり、
\(\textrm{AD}=\textrm{BD}=x\)
∴ \(\textrm{CD}=1-\textrm{AD}\)\(=1-x\)
\(△\textrm{ABC}\) ∽ \(△\textrm{BCD}\) より、
\[\begin{split}&\textrm{BC}:\textrm{AB}=\textrm{CD}:\textrm{BC}\\\Leftrightarrow\:\:&x:1=(1-x):x\\\Leftrightarrow\:\:&x^2=1-x\\\Leftrightarrow\:\:&x^2+x-1=0\end{split}\]
\(x>0\) より、解の公式から、
\(x=\displaystyle\frac{-1+\sqrt{5}}{2}\) (答)
(3)
図の直角三角形 \(\textrm{AHD}\) に注目することで、
\(\cos36^\circ=\displaystyle\frac{\textrm{AH}}{\textrm{AD}}\:\)\(=\displaystyle\frac{\displaystyle\frac{1}{2}}{\displaystyle\frac{-1+\sqrt{5}}{2}}\:\)\(=\displaystyle\frac{1}{\sqrt{5}-1}\:\)\(=\displaystyle\frac{\sqrt{5}+1}{4}\) (答)
これまでの記事の内容を知ってれば、間違えようがないでしょ?
とゆーわけで、ここからは大学受験数学で知っておいた方がいいcos36°の導出を紹介していきます。
- 文理共通範囲でのcos36°の導出
- 理系専用範囲でのcos36°の導出



ここからは、\(36^\circ=\displaystyle\frac{\pi}{5}=\theta\) として、特に断りなく \(\cos36^\circ=\cos\theta=c\:,\:\)\(\sin36^\circ=\sin\theta=s\) って書いちゃうね


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
文理共通範囲でのcos36°の導出
正五角形の利用
概要
前々回の記事の『正五角形』から前回の記事冒頭の流れ、と同様の導出ですが、ここでは『トレミーの定理』を用いて、正五角形の対角線を時短で求める方法を紹介します。



5年前くらいに先輩が教えてくれた(笑)
導出
一辺の長さが1、対角線長さが \(l\) の正五角形 \(\textrm{ABCDE}\) について、\(∠\textrm{BAC}=108^\circ\:,\:\:\)\(∠\textrm{ABC}=\displaystyle\frac{180^\circ-108^\circ}{2}=36^\circ\) である。


四角形 \(\textrm{BCDE}\) は円に内接するので、トレミーの定理より、
\(l\cdot l\:\)\(\:=\:\)\(\:l\cdot1+1\cdot1\)
\[\Leftrightarrow\:\:l^2-l-1=0\]
\(l>0\) より、解の公式から、\[l=\displaystyle\frac{1+\sqrt{5}}{2}\]
上図の直角三角形に注目することで、
\[\cos36^\circ=\displaystyle\frac{l}{2}=\frac{1+\sqrt{5}}{4}\]
2倍角と3倍角の公式の併用(チェビシェフ多項式)
概要
\(\theta=36^\circ=\displaystyle\frac{\pi}{5}\) は5倍することで有名角 \(180^\circ=\pi\) となります。
文理共通範囲では5倍角の公式の導出が面倒なため、5=2+3より、暗記が推奨されている2倍角と3倍角の公式で \(180^\circ=\pi\) を登場させる方法が有名です。



2倍角と3倍角の公式を覚えてない人、必ず暗記しておこう!
2倍角の公式
\[\begin{split}\sin2\alpha&=2\sin\alpha\cos\alpha\\\cos2\alpha&=\cos^2\alpha-\sin^2\alpha\\&=1-2\sin^2\alpha\\&=2\cos^2\alpha-1\end{split}\]



↑は加法定理からすぐに導けるけど、良く使うから全部丸暗記
3倍角の公式
\(\sin3\alpha=\:\)\(3\:\)\(\sin\:\)\(\alpha\:\)\(-\:\)\(4\:\)\(\sin\)\(^3\)\(\:\alpha\)
サンシャインひいて夜風が身にしみる
\(\cos3\alpha=\:\)\(4\:\)\(\cos\)\(^3\)\(\:\alpha\:\)\(-\:\)\(3\:\)\(\cos\:\)\(\alpha\:\)
ヨウコさん、さあこすりましょう



↑は使用頻度は高くないけど、できる人は暗記しておくのが普通
cosの3倍角の語呂合わせを授業で教えると…
男どもが「下ネタだ~」って喜びだすんだけど…(笑)



変な想像するな!こっち↓の「こする」だっ!!


下図の対称性(補角公式でも良い)から、
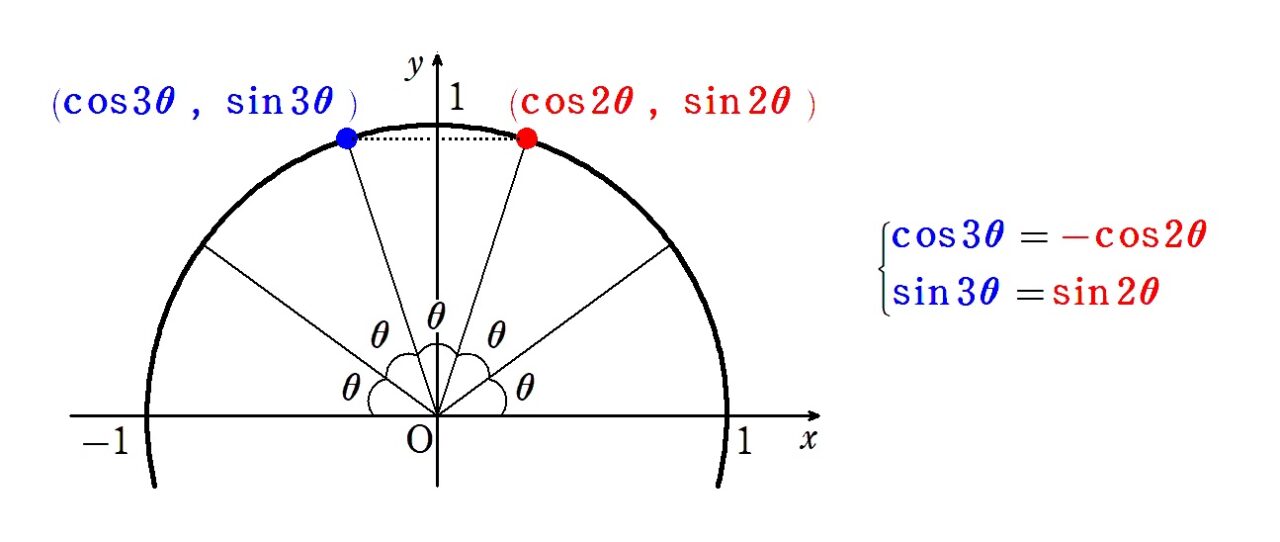

誘導がつく場合はcosでの立式が要されるケースの方が多いんだけど、自分で導くときはsinの方が楽です。



チェビシェフ多項式では、\(n\) を自然数として \(\sin n\alpha\) が \(\sin\alpha\) でくくれることを約束してるから、sinで立式するとすぐに \(\sin\theta\) で割れて楽なんだよね。
この文章は理解しなくてもオッケー。チェビシェフって言葉も覚えなくてオッケー(笑)
導出
\(\theta=36^\circ\) について、
\[\begin{split}\sin3\theta&=\sin(180^\circ-2\theta)\\&=\sin2\theta\end{split}\]



左辺に「サンシャインひいて夜風が身にしみる」、右辺に2倍角の公式を使うよ!
よって、
\[3\sin\theta-4\sin^3\theta=2\sin\theta\cos\theta\]
\(\sin\theta\neq0\) より、
\[\begin{split}&3-4\sin^2\theta=2\cos\theta\\\Leftrightarrow\:\:&3-4(1-c^2)=2c\\\Leftrightarrow\:\:&4c^2-2c-1=0\end{split}\]
\(c>0\) より、解の公式から、
\[c=\cos36^\circ=\displaystyle\frac{1+\sqrt{5}}{4}\]
理系専用範囲でのcos36°の導出
執筆時2022年度では完全に理系専用範囲の「複素数平面」の知識を用いた導出も有名です。
極形式で5倍角の公式を立式
概要
前項で「文理共通範囲では5倍角の公式の導出が面倒」と言いましたが、理系専用範囲の「極形式」と「ド・モアブルの定理」を用いれば、比較的簡単に5倍角の公式を導くことができます。
ド・モアブルの定理
任意の整数 \(n\) に対して、
\[(\cos\alpha+i\sin\alpha)^n=\cos n\alpha+i\sin n\alpha\]
が成立する



ここでは極形式 \(z=r(\cos\alpha+i\sin\alpha)\)(\(r>0\))の絶対値 \(r=1\) にした簡単バージョンしか使わないので、↑のみ紹介します。加法定理の逆利用で証明できるけど、これも割愛(笑)
「二項定理」も使うので一応紹介しますが…



「二項定理」なんて暗記する価値もないよ(笑)
高校入ってからすぐに、絶対暗記させられる展開公式
\((a+b)^3=a^3+\:\)\(3\)\(a^2b+3ab^2+b^3\)
の各項の次数は全て3だよね?これは、
\((a+b)^3=(a+b)(a+b)(a+b)\)
ってゆー3つのカッコ1つずつから \(a\) と \(b\) のどっちかを持ってきて展開してるから。



じゃあ次に上の \(3\) の意味を考えてみよう!
\(a^2b\) は \(b\) を1個持ってきてる。
\(b\) を3つのどのカッコから持ってくるかで \({}_3\mathrm{C}_1=3\) ってこと。



「二項定理」ってのは、これをn乗に拡張しただけ。
n個のカッコをイメージしよう!
\(b\) を \(0\) 個持ってきた場合、\(a\) は \(n\) 個で、\(b\) を持ってくるカッコの選び方は \({}_n\mathrm{C}_0\)
\(b\) を \(1\) 個持ってきた場合、\(a\) は \(n-1\) 個で、\(b\) を持ってくるカッコの選び方は \({}_n\mathrm{C}_1\)
\(b\) を \(2\) 個持ってきた場合、\(a\) は \(n-2\) 個で、\(b\) を持ってくるカッコの選び方は \({}_n\mathrm{C}_2\)
:
:
:
\(b\) を \(n-1\) 個持ってきた場合、\(a\) は \(1\) 個で、\(b\) を持ってくるカッコの選び方は \({}_n\mathrm{C}_{n-1}\)
\(b\) を \(n\) 個持ってきた場合、\(a\) は \(0\) 個で、\(b\) を持ってくるカッコの選び方は \({}_n\mathrm{C}_n\)
↓
二項定理
\(n\) を自然数とすると、
\((a+b)^n\)\(\:={}_n\mathrm{C}_0a^n+{}_n\mathrm{C}_1a^{n-1}b+{}_n\mathrm{C}_2a^{n-2}b^2\)\(\:+\:\cdots\cdots\)
\(\:+\:{}_n\mathrm{C}_{n-1}ab^{n-1}+{}_n\mathrm{C}_nb^n\)



「二項定理」の証明が出題された場合、上の流れを書ければオッケーとされています!僕は一応帰納法で証明するけど(笑)
全体の流れとしては、
左辺を「二項定理」で展開して、両辺の実部(\(i\) がついてないとこ)と虚部(\(i\) がついてるとこ)を比較するんだけど…



因みに、虚数単位 \(i\) について、\(i^2=-1\)
次のSTEPから言って、ほぼほぼsinの方しか考えさせない誘導がほとんどです。



実部まで考えてたら、ムダな項が多くなって大変だよ!
同じ流れで7倍角の公式を導かせる誘導も頻出(2016横浜市立大医学部)だけど、これで実部まで考えてたら終わっちゃう。
この記事ではもう \(36^\circ=\displaystyle\frac{\pi}{5}=\theta\) にしちゃってるけどね(笑)
実際に誘導に従って解いてる場合は、この時点で \(5\theta\) に (整数) \(\pi\) を当てはめます。



単位円ですぐ分かるけど、「\(\sin\) (整数) \(\pi=0\)」は暗記しておいた方がいいよ!三角関数の積分でチョー役に立つ
これで \(5\theta\) が消えて \(\theta=36^\circ\) のみの式の完成です。
って感じなんですが、ほぼ作業化しておけるのが理想です。



受験直前に2016横浜市立大医学部の問題やらせた生徒が、2018東海大医学部でまんま出て、医学部一校しか受けてないのにマグレで医学部生になれました(笑)
導出
ド・モアブルの定理から、
\[(\cos\theta+i\sin\theta)^5=\cos5\theta+i\sin5\theta\]



左辺の展開では5個のカッコをイメージして!
\(i^2=-1\) だから、虚部は \(i\sin\theta\) を奇数個持ってきたときにできるよ!
この両辺の虚部に注目することで、
\({}_5\mathrm{C}_1\cos^4\theta(i\sin\theta)+{}_5\mathrm{C}_3\cos^2\theta(i\sin\theta)^3\:\)\(+{}_5\mathrm{C}_5(i\sin\theta)^5=i\sin5\theta\)
両辺を \(i\) で割って、
\(5\cos^4\theta\sin\theta-10\cos^2\theta\sin^3\theta+\sin^5\theta=\sin5\theta\)
ここで、\(\theta=36^\circ\) より \(\sin5\theta=\sin180^\circ=0\) 、また \(\sin\theta\neq0\) であるから、
\[\begin{split}&5\cos^4\theta-10\cos^2\theta\sin^2\theta+\sin^4\theta=0\\\Leftrightarrow\:\:&5c^4-10c^2(1-c^2)+(1-c^2)^2=0\\\Leftrightarrow\:\:&16c^4-12c^2+1=0\end{split}\]
解の公式より、
\[c^2=\displaystyle\frac{6\pm\sqrt{20}}{16}\]
\(c>0\) から、
\[\begin{split}c&=\displaystyle\frac{\sqrt{6\pm2\sqrt{5}}}{4}=\frac{\sqrt{(\sqrt{5}\pm1)^2}}{4}\\&=\frac{\sqrt{5}\pm1}{4}\end{split}\]
\(c=\cos36^\circ>\cos45^\circ=\displaystyle\frac{\sqrt{2}}{2}\) より、
\[\cos36^\circ=\displaystyle\frac{1+\sqrt{5}}{4}\]
1の5乗根の利用
概要
方程式 \(x^5=1\) の解を「1の5乗根」と呼びます。



複素数平面上で、「単位円に内接し、点1を頂点の1つとする正五角形の頂点」になったりするんだよ。今回の記事では割愛するけど(笑)
これと前項で紹介した「ド・モアブルの定理」を活用することでcos36°を求めることも可能です。



でも受験でこの誘導がつく場合、cos72°やcos144°を求めることがほとんど
なので、ここではcos72°を求めてから、
半角公式
\[\begin{split}&\sin^2\alpha=\displaystyle\frac{1-\cos2\alpha}{2}\\&\cos^2\alpha=\frac{1+\cos2\alpha}{2}\\&\sin\alpha\cos\alpha=\frac{\sin2\alpha}{2}\end{split}\]
でcos36°を導くことにします。
因みに「半角公式」は、先に紹介した「2倍角の公式」を変形しただけですが…
三角関数の次数を下げてくれるから、
「半角公式」が三角関数の公式の中で一番重要
です。



「半角公式」を覚えてないなら、数学使って受験しちゃダメ!
金のムダ
他にここで使う知識は2つ。
有名因数分解公式
\(n\) を自然数とすると、
\(x^n-y^n\)\(\:=(x-y)(x^{n-1}+x^{n-2}y+x^{n-3}y^2\)\(\:+\:\cdots\cdots\:+xy^{n-2}+y^{n-1})\)
「1の5乗根」の場合は \(y\) に1を当てはめて簡略化した、
\(x^n-1\)\(\:=(x-1)(x^{n-1}+x^{n-2}+x^{n-3}\)\(\:+\:\cdots\cdots\:+x+1)\)
を覚えてればいいんだけど…



前回の記事のここだと「-1の5乗根」だから、\(y\) に-1を当てはめてるんだよね…
だから \(x^n-y^n\) で暗記しておくのがベスト。



証明には等比数列の和の公式を使うんだけど、既にこの記事長くなりすぎだから割愛します(笑)
相反型4次方程式の解法
\(a\)\(x^4+\:\)\(b\)\(x^3+\:\)\(c\)\(x^2+\:\)\(b\)\(x+\:\)\(a\)\(\:=0\)
し・ん・ぶ・ん・し
って係数の4次方程式を見たら、\(x\neq0\) を確認してから、
\(x^2\) で割って、\(x+\displaystyle\frac{1}{x}=t\)
っておいとけば、\(x^2+\displaystyle\frac{1}{x^2}=t^2-2\) になっていい感じ
2018慶應義塾大理工の一番最初で出題されているくらい有名です。



合格者で解けなかった人はいないはず(笑)
こんなの自分で思いつかないでしょ?だから暗記
因みに「1の7乗根」もたまに出題されますが、相反型6次になるので \(x^3\) で割ります。



\(a\) を定数として \(〇\left(a^{2x}+\displaystyle\frac{1}{a^{2x}}\right)\)\(\:+△\left(a^x+\displaystyle\frac{1}{a^x}\right)\)\(\:+\:▢\) って形の最大・最小って超頻出なんだけど、これも \(a^x+\displaystyle\frac{1}{a^x}=t\) っておいて、\(a^{2x}+\displaystyle\frac{1}{a^{2x}}=t^2-2\) にして2次関数に持ち込みます。関連させて覚えとくのがベスト
導出
\(x=\cos72^\circ+i\sin72^\circ\) について、ド・モアブルの定理から、
\(x^5=\cos360^\circ+i\sin360^\circ=1\)
∴ \(x^5-1=0\)



「有名因数分解公式」を使うよ!
\[\Leftrightarrow\:\:(x-1)(x^4+x^3+x^2+x+1)=0\]
\(x\neq1\) より、
\[x^4+x^3+x^2+x+1=0\]



全部係数は1で「し・ん・ぶ・ん・し」の4次方程式だから…
\(x\neq0\) より、
\[\begin{split}&x^2+x+1+\displaystyle\frac{1}{x}+\frac{1}{x^2}=0\\\Leftrightarrow\:\:&\left(x^2+\frac{1}{x^2}\right)+\left(x+\frac{1}{x}\right)+1=0\end{split}\]
ここで \(x+\displaystyle\frac{1}{x}=t\) とおくと、\(x^2+\displaystyle\frac{1}{x^2}=t^2-2\) より、
\[\begin{split}&t^2-2+t+1=0\\\Leftrightarrow\:\:&t^2+t-1=0\end{split}\]
解の公式から、
\[t=\displaystyle\frac{-1\pm\sqrt{5}}{2}\]
ここで、
\[\begin{split}t&=x+\displaystyle\frac{1}{x}\\&=\cos72^\circ+i\sin72^\circ+\frac{1}{\cos72^\circ+i\sin72^\circ}\\&=\cos72^\circ+i\sin72^\circ+\cos{\small(-72^\circ)}+i\sin{\small(-72^\circ)}\\&=\cos72^\circ+i\sin72^\circ+\cos72^\circ-i\sin72^\circ\\&=2\cos72^\circ\end{split}\]
\(\cos72^\circ>0\) より、
\[\cos72^\circ=\displaystyle\frac{t}{2}=\frac{-1+\sqrt{5}}{4}\]



「半角公式」を使って終了
よって、
\[\begin{split}\cos^236^\circ&=\displaystyle\frac{1+\cos72^\circ}{2}=\frac{1+\displaystyle\frac{-1+\sqrt{5}}{4}}{2}\\&=\frac{3+\sqrt{5}}{8}=\frac{6+2\sqrt{5}}{16}\\&=\left(\frac{\sqrt{5}+1}{4}\right)^2\end{split}\]
\(\cos36^\circ>0\) より、
\[\cos36^\circ=\displaystyle\frac{1+\sqrt{5}}{4}\]
まとめ
ここで扱った4つ(文系なら2つ)のcos36°の導出を自分でできるようにしておけば、大学受験で出題されたときに完勝間違いなし!



細かいとこまで丸暗記する必要はないよ!
誘導に乗れれば問題ないから
やっぱり凄い長い記事になっちゃったな~、今度こそ短くするつもりだったんだけどね(笑)
申し訳ないm(_ _)m
君の大学受験が最高の結果になることを祈ってます!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。








