cos36°は良い子(4・1・5)
.jpg)
こーゆー小手先のテクニックは好きではありませんが…
 めぐろ塾の安田
めぐろ塾の安田特に医学部受験生は覚えちゃった方が良い
結論:cos36°は良い子(4・1・5)
前回の記事の内容から、cos36°=…





上の記事の…
赤の直角三角形に注目すれば、「〇」= \(\cos36^\circ\) であることが分かります。
また、\(l\) は線分マーク「〇」の2つ分なので、
\[\cos36^\circ=\displaystyle\frac{l}{2}=\displaystyle\frac{1+\sqrt{5}}{4}\]



cos36°の結果として登場する値が、「良い子(4・1・5)」であることが分かったね!
何で「良い子(4・1・5)」って覚えるの?
大学受験数学でのマーク式の解答方法の多くは、0~9の数字のマークです。





共通テストとかも採用してるこの形。だから「cos36°は良い子(4・1・5)」って覚えておけば…






ですぐに埋められちゃうんですよ…



何たる小手先テクニック!(笑)
因みに、2倍角の公式 \(\cos2\theta=2\cos^2\theta-1\) や、単位円から当たり前に導かれる
- 余角公式 \(\sin(90^\circ-\theta)=\cos\theta\)
- 補角公式 \(\cos(180^\circ-\theta)=-\cos\theta\:,\:\:\)\(\sin(180^\circ-\theta)=\sin\theta\)
も利用すると、0°から180°までの三角比では、
\[\cos36^\circ=\sin54^\circ=\sin126^\circ=\displaystyle\frac{1+\sqrt{5}}{4}\:,\]
\[\cos72^\circ=\sin18^\circ=\sin162^\circ=\displaystyle\frac{-1+\sqrt{5}}{4}\:,\]
\[\cos108^\circ=\displaystyle\frac{1-\sqrt{5}}{4}\:,\]
\[\cos144^\circ=\displaystyle\frac{-1-\sqrt{5}}{4}\]
も似たような形になるので、0~9の数字のマークであれば、これらも何も考えずに「良い子(4・1・5)」で答を当てられてしまいます。
\(\displaystyle\frac{\pi}{5}=36^\circ\) や \(\displaystyle\frac{\pi}{10}=18^\circ\) 系の \(\sin\:,\:\cos\) に出会ったら、
取りあえず「cos36°は良い子(4・1・5)」って唱える
こと
黄金比も覚えやすくなる!
この人なんて薄っぺらいこと話してるんだろう…
って思った人もいるでしょう。



自分でもそう思う(笑)
でもバカにするなかれ。
前回の記事で、正五角形の一辺と対角線の長さの比(黄金比)は値を暗記しておくのがオススメと言いましたが…
「cos36°は良い子(4・1・5)」を覚えておくと、黄金比が圧倒的に覚えやすくなるんですよね。
ちょっとでも冒頭の対応を思い出せれば、「良い子(4・1・5)」の2倍で、


って埋められちゃうでしょ?



これも語呂合わせで「にいこ(2・1・5)」ってしちゃおうか
ルートの中の候補として5以外に2も入るので、「cos36°は良い子(4・1・5)」ほど強力な語呂合わせではありません。



でも \(l=\displaystyle\frac{1+\sqrt{2}}{5}\) って埋めたら明らかに一辺の長さ1を下回っちゃうから…流石に間違えないっしょ(笑)
「cos36°は良い子(4・1・5)」って唱えると共に、
「にいこ(2・1・5)」にしてね~だろ~な~?
って疑うこと


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
医学部受験での活用例
すんげーテクニックを知っちまったぜぇえええええええええええええー!!!



なんて感動して欲しくもない(笑)
近年の医学部受験で言うと、「もし出題された場合、知らなかったらそもそも勝負にならない」って感じなんですよね。
いくつか具体例を。
- 医学部受験での活用例
2014東邦大医学部
90分で15問。その中の1問として出題された問題です。
問題


解説
マーク式で「正五角形」なので、「cos36°は良い子(4・1・5)」って唱えると共に「にいこ(2・1・5)」を疑いましょう。



\(\displaystyle\frac{1+\sqrt{5}}{4}<1\:,\:\displaystyle\frac{1+\sqrt{5}}{2}>1\)
外接円の半径の方が大きいに決まってんだから、1より小さい値を解答するに決まってんじゃん
だから、「良い子(4・1・5)」。





流石にもうちょっとまともな説明も入れとくね(笑)
前回の記事の『円に内接するn角形』で説明した内容から、下図を作図します。
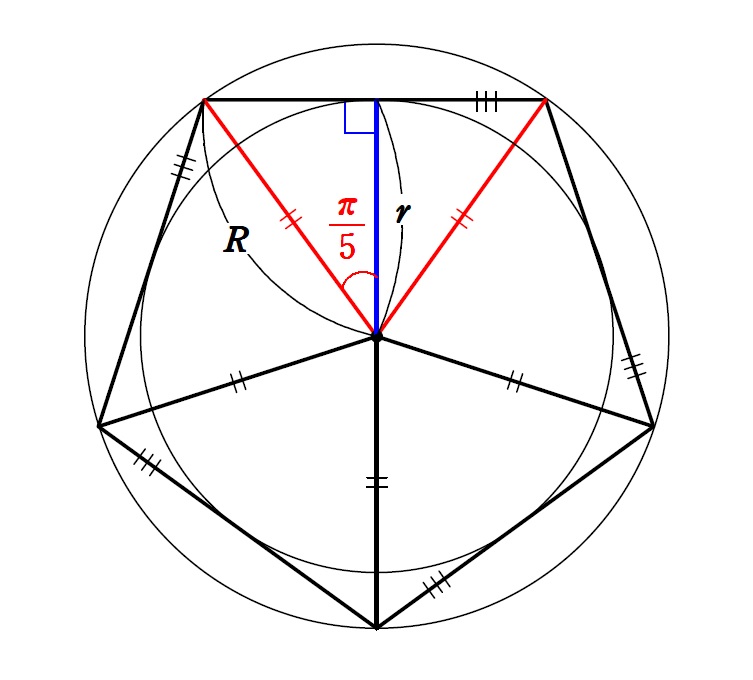

この図の直角三角形に注目することで、
\(r=R\cos\displaystyle\frac{\pi}{5}\) ∴ \(\displaystyle\frac{r}{R}=\cos\frac{\pi}{5}=\cos36^\circ\)
なので、「良い子(4・1・5)」に間違いありません。
実際に作図する二等辺三角形は1つで十分です。
ってゆーか、できる人は外接円すら描きません。



二等辺1つだけ描いて、半分に割った直角三角形にすぐに斜角 \(\displaystyle\frac{\pi}{5}\) と斜辺に \(R\) 、底辺に \(r\) を書き込んじゃう、条件反射で(笑)
講評
この頃の東邦大医学部は、プロでも



時間足りねー…
って鬼畜仕様(笑)
90分15問で、一問あたり6分しか使えないんですが、かなり難易度高い・計算面倒な問題も含まれてまして…
「満点は諦めて最低10問当てる、そこから何問上積みできるか」の勝負でした。
この2014年度は、偏差値73の生徒と時間内で勝負したんで凄い覚えてるんですが…



その生徒がこの問題捨てていて10完以下、この問題10秒で完答したオレは2~3ミスで乗り切って、えらそーにマウントとってやった(笑)
でも安心してください!
2017以降の東邦大医学部は、試験時間90分は変わらず、問題数は10問に減少しています!



2017は一応満点とれた、上の生徒も満点だった(笑)
ま~その分合格点は上がってると思うので、喜んではいられませんが。
逆に「数学で差がつきにくくなった」とも言えるので、数学できる人からすると悲報です。
2016・2021順天堂大医学部
2016大問Ⅱ前半
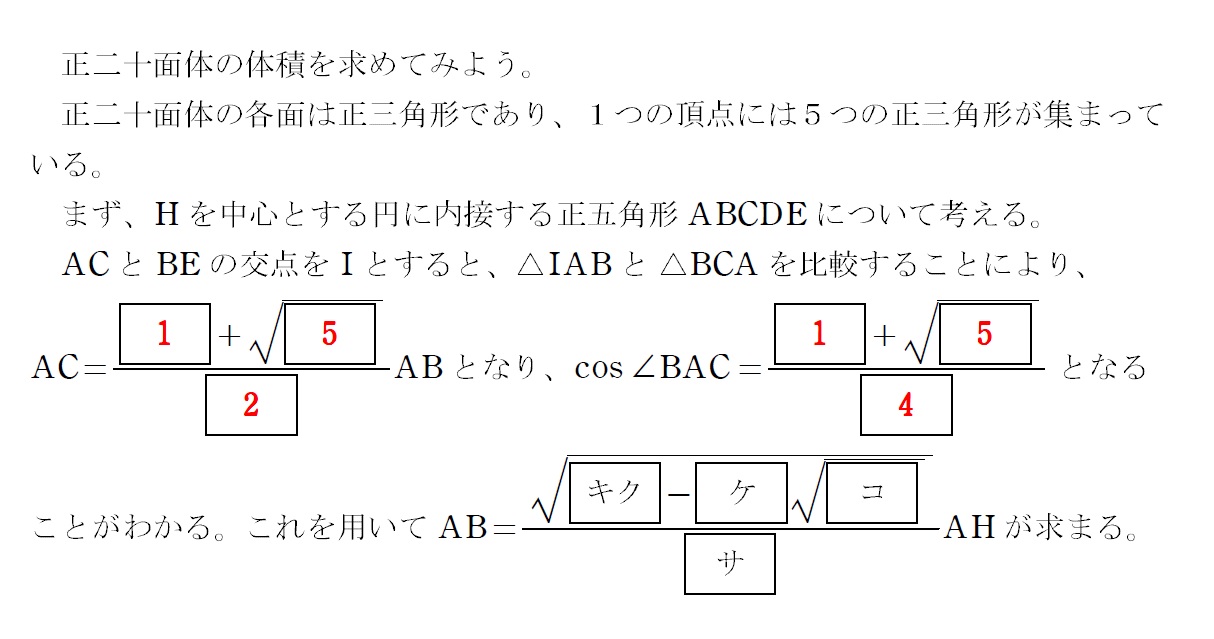

掲載してるのは大問Ⅱの文章全体の1/3くらいです。
2021大問Ⅱ(a)
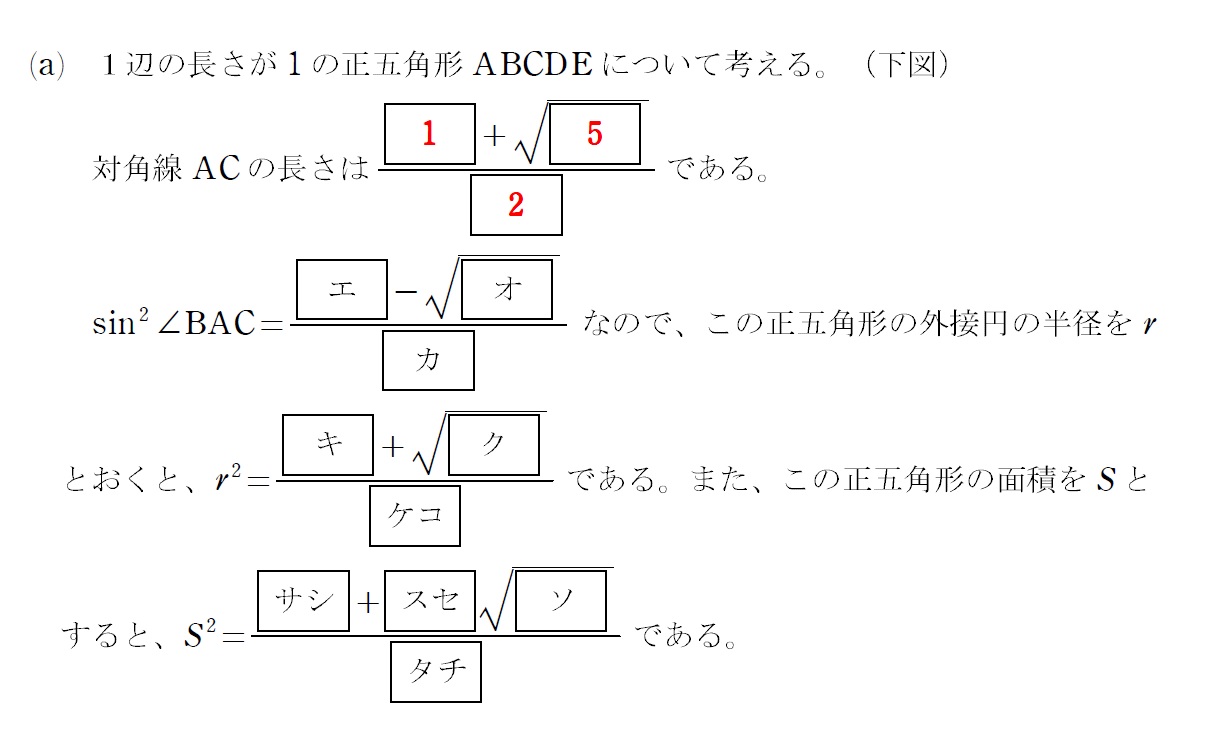

(b)と(c)もあるので、やはり全体の1/3くらいです。



やはりもう穴埋めしといた(笑)一辺の長さ1の正五角形の対角線の長さだから「にいこ(2・1・5)」ね!
因みにその後は、
- 冒頭の対応からcos∠BAC=「cos36°は良い子(4・1・5)」を出し、\(\sin^2∠\textrm{BAC}=1-\cos^2∠\textrm{BAC}\)
- △ABCに正弦定理 \(\displaystyle\frac{\textrm{BC}}{\sin∠\textrm{BAC}}=2r\) で \(r^2\) を出す
- 前回の記事の『円に内接するn角形』の内容から正五角形を二等辺三角形5つに分割し、\(S=\displaystyle\frac{1}{2}r^2\sin\frac{2\pi}{5}\times5\) で計算
で穴埋めていきます。
順天堂大医学部の数学について
試験時間70分。大問構成は2003から以下の通りで、2022現在も変わっていません。
| 大問 | 形式 |
|---|---|
| Ⅰ | マーク式小問集合。 2015以降は3~4題。設問ごとの難易度差が激しい。簡単な問題は本当に簡単だが、国立大問レベルがネタにされることもあり。 |
| Ⅱ | マーク式大問 |
| Ⅲ | 記述式大問 |
今回挙げた2016周辺は難易度がやばかったんですよね…



人間が時間内に終わるように作問してくれてない(笑)
2018以降は大分まともに点数とれる感じに戻りましたが、それでも満点は望んじゃいけないレベルです。
順天堂大医学部の数学では、
ここで1問外してもしょうがない。



メンタルを強く持て!
記述式だから部分点を獲得しやすいので。



全部解けると思うな!ひたすら部分点を取れ!必ずちょっとは時間を残して…



たまに「大問Ⅱは丸々捨てちゃった方が良くね?」って年もある(笑)
- マーク式だから部分点が望めない
- 歴史的に大問Ⅱに難易度が高すぎる問題を設置することが多い
ってとこから後回し。
でも難易度高すぎる問題の場合も、最初のいくつかは当てられるレベルにしてくれるから、これの取りこぼしはないように!
って解く順番を決めといてしまった方がいいように思えます。



今回挙げた2021は大問Ⅱより大問Ⅲの方が難しかったけど(笑)でも大問Ⅲで「全部解けると思うな!」ってことを認識してれば、大問Ⅱにある程度の時間を残せたと思う
今回の記事のテクニックは、STEP3での点数上積みのための必須テクニックです。
知らなかったら、順天では勝負にすらなりません。
おいおい、正二十面体って…
2016の最初の「正二十面体の体積を求めよう。」って文章でメンタル折られた受験生も多いと思います(笑)



問題文で立体図与えてくれてないんだけど…自分で作図するのムリだよね(笑)正十二面体なら一点に集まる正五角形が3枚だから、描けなくはないレベルだけど
長いので問題文を最後まで掲載しませんでしたが、「立体は断面を抜き出して考える」ってゆー本質に従った誘導は付いてるものの計算量も多く、途中当てカンで当てられる部分があるにせよ、完答できた受験生はほとんどいなかったものと思われます。



調べた感じ、これ以前で正十二面体の計量だしてるのは2010の岐阜薬科大だけど、ここまで複雑な問題じゃないし、これ対策してた人もいないでしょ(笑)試験本番で完全初見の複雑な立体計量やらされた2016の受験生は可哀想…
今ちょっと登場しましたが、各面が正五角形なので、『正十二面体』でも「cos36°は良い子(4・1・5)」や「にいこ(2・1・5)」が有効です。
これらが使える問題ではありませんでしたが、『正十二面体』は2021共通テストⅡB第5問(ベクトル)でも題材にされています。
実は今回挙げた2021の順天の大問Ⅱも、最終的に(c)で正二十面体を考えさせています。
医学部受験業界では、2016の正二十面体の出題はそこそこ話題になりましたが、2021の正二十面体はあまり話題になりませんでした。
確かに2021の方が計算量が少ない、誘導が親切ってゆーのもあるんですが、それ以上に…



医学部受験業界全体に「順天は正二十面体の計量が好き」ってゆー耐性がついたことの方が大きいと思う(笑)
なので、順天堂大医学部の受験者は、正五角形の頂点の1つをA、外接円の中心をO、この正五角形を底面とする正五角錐の頂点をFとすると、
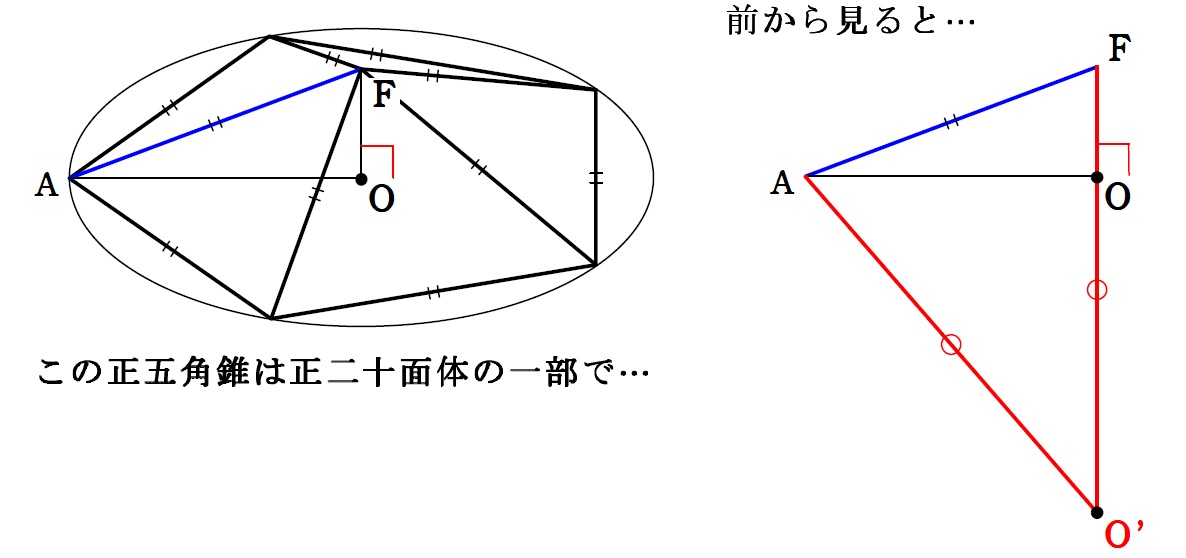

という、正二十面体の外接球の中心O’の作図を暗記しておくべきに思えます。



2021の受験生で、2016のこの作図をやってなかった人はメチャクチャ不利だったでしょう
2022東北医科薬科大医学部
軽く近年の医学部の過去問をほぼ全て流し見した感じでは、2018~2020で今回の記事のテクニックが有効な問題は出題されていませんでした。



残念(笑)でも執筆時最新年度でも…
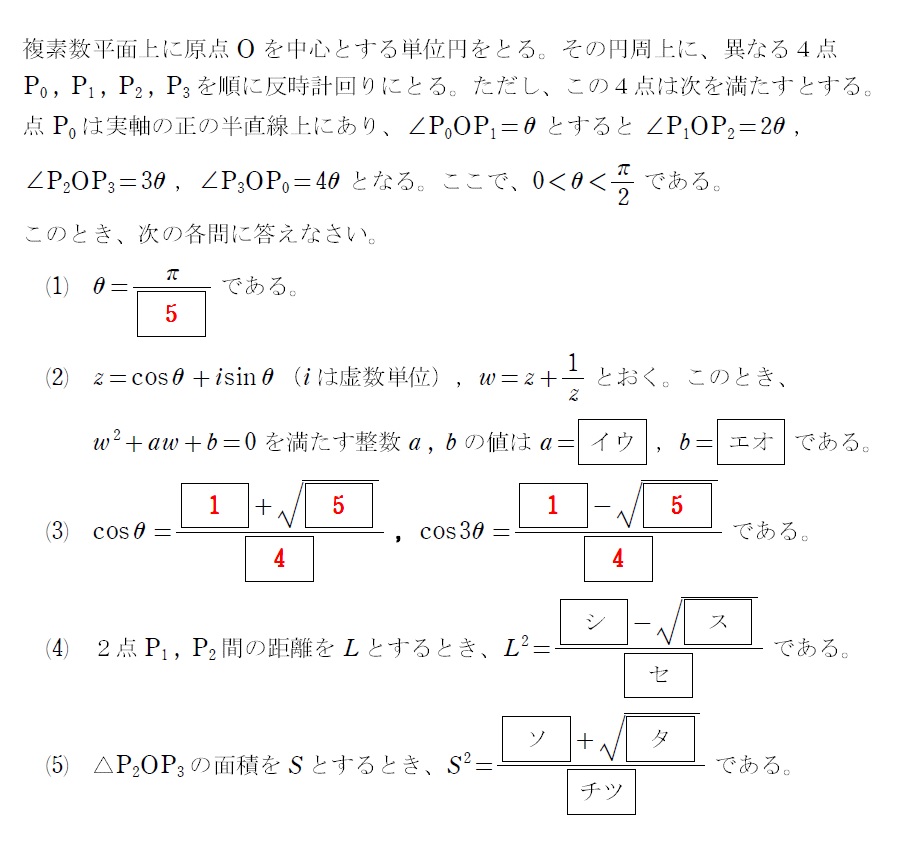




やはりもう穴埋めしときました
試験時間70分で、マーク式大問3つ。その中の大問の1つでした(第Ⅱ問、これは全文掲載します)。
(1) 序文をちょっと読めば、一周 \(2\pi=\theta+2\theta+3\theta+4\theta=10\theta\) で \(\theta=\displaystyle\frac{\pi}{5}=36^\circ\) が分かります。



この時点で(3)でしょ(笑)
(3) 「cos36°は良い子(4・1・5)」を発動して終了~



(2)の処理も、僕は生徒に「1のn乗根」の授業でほぼ暗記させるけどね(この次の記事↓で扱っています)


(2) \(z\) は \(-1\) の5乗根だから、\(z^5=-1\) 。因数分解して \(z\neq-1\) から \(z^4-z^3+z^2-z+1=0\)(相反型4次方程式)。\(z\neq0\) より両辺を \(z^2\) で割って、\(z^2+\displaystyle\frac{1}{z^2}=w^2-2\) から、\(w^2-w-1=0\) 。因みに厳密には(3)は、これに解の公式を用い、\(w=z+\displaystyle\frac{1}{z}\)\(=(\cos\theta+i\sin\theta)+\{\cos(-\theta)+i\sin(-\theta)\}\)\(=2\cos\theta\) から計算します。
(4) 余弦定理で \(L^2=1^2+1^2-2\cdot1\cdot1\cdot\cos2\theta\)\(=2-2(2\cos^2\theta-1)\)\(=\displaystyle\frac{5-\sqrt{5}}{2}\)
(5) \(S=\displaystyle\frac{1}{2}\sin3\theta\) から、\(S^2=\displaystyle\frac{1}{4}\sin^2 3\theta\)\(=\displaystyle\frac{1-\cos^2 3\theta}{4}\)\(=\displaystyle\frac{5+\sqrt{5}}{32}\)



この記事執筆するから一応僕も時間測って解いたけど、3分47秒でした!
…(4)の最後の引き算ミスったけど(笑)
優秀な医学部受験生なら、僕より速く、完璧に当ててくると思います。



2022は第Ⅲ問が難しかったよ。この問題は5分くらいで片付けて、第Ⅲ問に時間使えるようにするのがベスト!
まとめ
マーク式で \(\displaystyle\frac{\pi}{5}=36^\circ\) や \(\displaystyle\frac{\pi}{10}=18^\circ\) 系の \(\sin\:,\:\cos\) に出会ったら、取りあえず



「cos36°は良い子(4・1・5)」
って唱えて、正五角形の場合は、これを唱えると共に、



「にいこ(2・1・5)」にしてね~だろ~な~?
って疑うこと。
短くするつもりが今回も長くなっちゃった(笑)
君の大学受験が最高の結果になることを祈ってます!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。










